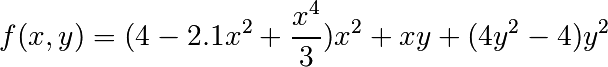I. Préambule▲
Ce tutoriel n'est en aucun cas une introduction au calcul scientifique. Vu que le nombre de sous-modules et de fonctions présents dans SciPy est très important, il serait fastidieux de rentrer dans les détails. Nous nous concentrerons donc sur quelques exemples pour vous donner une idée générale afin que vous puissiez utiliser SciPy pour implémenter les méthodes de calcul scientifique dont vous avez besoin.
SciPy est composée de sous-modules spéciaux :
Ils reposent tous sur NumPyhttp://docs.scipy.org/doc/numpy/reference/index.html#numpy, mais sont complètement indépendants les uns des autres. La manière standard pour importer la librairie NumPy et la librairie SciPy est la suivante :
>>> import numpy as np
>>> from scipy import stats # same for other sub-modulesL'import principal SciPy contient le plus souvent des fonctions identiques aux fonctions NumPy (comparer scipy.cos et np.cos). Celles-ci sont fournies uniquement pour des raisons historiques, il n'y a donc aucune raison d'effectuer un import scipy directement dans votre code.
II. Fichier entrée/sortie : scipy.io▲
- Chargement et enregistrement de fichiers Matlab :
>>> from scipy import io as spio
>>> a = np.ones((3, 3))
>>> spio.savemat('file.mat', {'a': a}) # savemat expects a dictionary
>>> data = spio.loadmat('file.mat', struct_as_record=True)
>>> data['a']
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])- Lecture d'images :
>>> from scipy import misc
>>> misc.imread('fname.png')
>>> # Matplotlib also has a similar function
>>> import matplotlib.pyplot as plt
>>> plt.imread('fname.png')Voir aussi :
- charger/enregistrer des fichiers texte : numpy.loadtxt()http://docs.scipy.org/doc/numpy/reference/generated/numpy.loadtxt.html#numpy.loadtxt/numpy.savetxt()http://docs.scipy.org/doc/numpy/reference/generated/numpy.savetxt.html#numpy.savetxt ;
- chargement « intelligent » de fichiers TEXT ou CSV : numpy.genfromtxt()http://docs.scipy.org/doc/numpy/reference/generated/numpy.genfromtxt.html#numpy.genfromtxt/numpy.recfromcsv() ;
- rapide et efficace, mais spécifique à NumPy, pour le format binaire : numpy.save()http://docs.scipy.org/doc/numpy/reference/generated/numpy.save.html#numpy.save/numpy.load()http://docs.scipy.org/doc/numpy/reference/generated/numpy.load.html#numpy.load.
III. Fonctions spéciales : scipy.special▲
Comme leurs noms l'indiquent, les fonctions spéciales ne sont pas des fonctions ordinaires. Les docstrings (ou « commentaires dans le code ») du module scipy.specialhttp://docs.scipy.org/doc/scipy/reference/special.html#scipy.special sont suffisamment bien détaillées pour ne pas en faire la liste ici.
Les fonctions les plus souvent utilisées sont :
- fonction de Bessel, comme scipy.special.jn() (fonction de Bessel d'ordre n) ;
- fonction elliptique (scipy.special.ellipj() pour la fonction Jacobienne elliptique) ;
- fonction Gamma : scipy.special.gamma(), aussi notée scipy.special.gammaln() qui donnera le logarithme du Gamma pour une précision numérique plus grande ;
- Erf, la surface sous une courbe de distribution gaussienne : scipy.special.erf().
IV. Opérations d'algèbre linéaire : scipy.linalg▲
Le module scipy.linalghttp://docs.scipy.org/doc/scipy/reference/linalg.html#scipy.linalg propose tout un tas d'opérations d'algèbre linéaire standards, reposant sur une implémentation qui a déjà fait ses preuves (BLAS, LAPACK).
- La fonction scipy.linalg.det()http://docs.scipy.org/doc/scipy/reference/generated/scipy.linalg.det.html#scipy.linalg.det calcule le déterminant de la matrice carrée :
>>> from scipy import linalg
>>> arr = np.array([[1, 2],
... [3, 4]])
>>> linalg.det(arr)
-2.0
>>> arr = np.array([[3, 2],
... [6, 4]])
>>> linalg.det(arr)
0.0
>>> linalg.det(np.ones((3, 4)))
Traceback (most recent call last):
...
ValueError: expected square matrix- La fonction scipy.linalg.inv()http://docs.scipy.org/doc/scipy/reference/generated/scipy.linalg.inv.html#scipy.linalg.inv calcule l'inverse de la matrice carrée :
>>> arr = np.array([[1, 2],
... [3, 4]])
>>> iarr = linalg.inv(arr)
>>> iarr
array([[-2. , 1. ],
[ 1.5, -0.5]])
>>> np.allclose(np.dot(arr, iarr), np.eye(2))
TrueEnfin, calculer l'inverse d'une matrice singulière (ou non inversible, car son déterminant est zéro) remontera l'erreur LinAlgError :
>>> arr = np.array([[3, 2],
... [6, 4]])
>>> linalg.inv(arr)
Traceback (most recent call last):
...
LinAlgError: singular matrix- Des opérations plus complexes sont disponibles, par exemple la méthode de décomposition en valeurs singulières (SVD) :
>>> arr = np.arange(9).reshape((3, 3)) + np.diag([1, 0, 1])
>>> uarr, spec, vharr = linalg.svd(arr)Le résultat de la décomposition est :
>>> spec
array([ 14.88982544, 0.45294236, 0.29654967])La matrice originale peut être recomposée en réalisant une multiplication matricielle des sorties de svd avec np.dot :
>>> sarr = np.diag(spec)
>>> svd_mat = uarr.dot(sarr).dot(vharr)
>>> np.allclose(svd_mat, arr)
TrueSVD est très souvent utilisée en statistiques et en traitement du signal. Beaucoup d'autres méthodes de décomposition standard (QR, LU, Cholesky, Schur), ainsi que des méthodes de résolution de systèmes linéaires sont également disponibles dans scipy.linalghttp://docs.scipy.org/doc/scipy/reference/linalg.html#scipy.linalg.
V. Transformées de Fourier (FFT) : scipy.fftpack▲
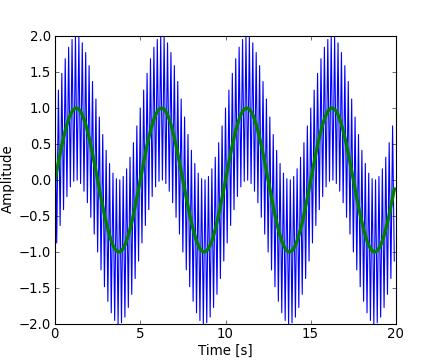
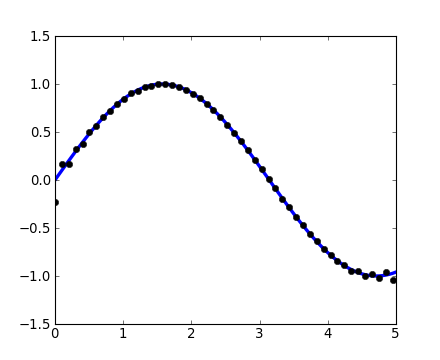
Le module http://docs.scipy.org/doc/scipy/reference/fftpack.html#scipy.fftpackhttp://docs.scipy.org/doc/scipy/reference/fftpack.html#scipy.fftpack permet de calculer des transformées de Fourier. Comme dans l'illustration, un signal d'entrée bruité pourrait ressembler à :
>>> time_step = 0.02
>>> period = 5.
>>> time_vec = np.arange(0, 20, time_step)
>>> sig = np.sin(2 * np.pi / period * time_vec) + \
... 0.5 * np.random.randn(time_vec.size)L'observateur ne connaît pas la fréquence du signal, mais uniquement la fréquence d'échantillonnage (échantillonnage dans le domaine temporel) du signal sig. Le signal est supposé provenir d'une fonction réelle de telle sorte que la transformée de Fourier soit symétrique. La fonction scipy.fftpack.fftfreq()http://docs.scipy.org/doc/scipy/reference/generated/scipy.fftpack.fftfreq.html#scipy.fftpack.fftfreq va générer les fréquences d'échantillonnage et scipy.fftpack.fft()http://docs.scipy.org/doc/scipy/reference/generated/scipy.fftpack.fft.html#scipy.fftpack.fft va calculer la transformée de Fourier.
>>> from scipy import fftpack
>>> sample_freq = fftpack.fftfreq(sig.size, d=time_step)
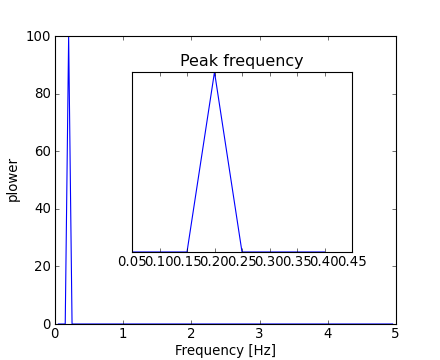
>>> sig_fft = fftpack.fft(sig)Parce que la puissance (power) résultante est symétrique, seule la partie positive du spectre suffira à trouver la fréquence :
>>> pidxs = np.where(sample_freq > 0)
>>> freqs = sample_freq[pidxs]
>>> power = np.abs(sig_fft)[pidxs]La fréquence du signal peut être obtenue ainsi :
>>> freq = freqs[power.argmax()]
>>> np.allclose(freq, 1./period) # check that correct freq is found
TrueÀ présent, le bruit haute fréquence va être supprimé à partir du signal de la transformée de Fourier :
>>> sig_fft[np.abs(sample_freq) > freq] = 0Le signal filtré résultant peut être obtenu par la fonction de Fourier inverse scipy.fftpack.ifft()http://docs.scipy.org/doc/scipy/reference/generated/scipy.fftpack.ifft.html#scipy.fftpack.ifft :
>>> main_sig = fftpack.ifft(sig_fft)Le résultat sera visible avec :
>>> import pylab as plt
>>> plt.figure()
>>> plt.plot(time_vec, sig)
>>> plt.plot(time_vec, main_sig, linewidth=3)
>>> plt.xlabel('Time [s]')
>>> plt.ylabel('Amplitude')numpy.ffthttp://docs.scipy.org/doc/numpy/reference/routines.fft.html#numpy.fft
Numpy propose également une implémentation de FFT (numpy.fft). Toutefois, nous vous conseillons de travailler avec celle du module SciPy qui se veut plus performante.
Exemple : recherche rudimentaire de période
Exercice : suppression du bruit d'une image d'alunissage
- Examinez l'image donnée moonlanding.png, qui est fortement contaminée par un bruit périodique. Dans cet exercice, nous souhaitons nettoyer le bruit en utilisant les transformées de Fourier.
- Chargez l'image en utilisant pylab.imread().
- Trouvez et utilisez la fonction FFT en 2D dans le module scipy.fftpackhttp://docs.scipy.org/doc/scipy/reference/fftpack.html#scipy.fftpack et affichez le spectre (la transformée de Fourier) de l'image. Avez-vous des difficultés à visualiser le spectre ? Si oui, pour quelles raisons ?
- Le spectre est constitué de hautes et basses composantes de fréquences. Le bruit est contenu dans la partie des hautes fréquences du spectre, fixez donc certaines de ces fréquences à zéro en utilisant un découpage approprié (array slicing).
- Appliquez la transformée de Fourier inverse et regardez l'image qui en résulte.
VI. Optimisation et Approximation : scipy.optimize▲
L'optimisation est le procédé numérique de recherche d'un extremum ou d'un point d'inflexion d'une fonction (c.-à-d. les points où le gradient de la fonction est nul).
Le module scipy.optimizehttp://docs.scipy.org/doc/scipy/reference/optimize.html#scipy.optimize propose de nombreux algorithmes très utiles pour la recherche de minimum de fonctions (scalaires ou multidimensionnelles), l'approximation de courbes et la recherche des racines.
>>> from scipy import optimizeTrouver le minimum d'une fonction scalaire
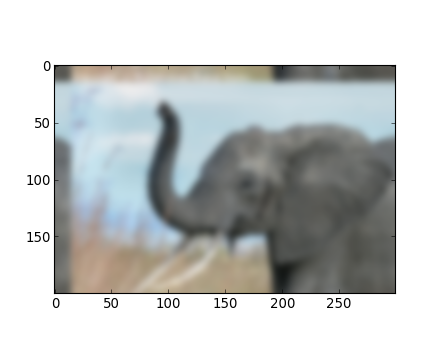
On définit la fonction suivante :
>>> def f(x):
... return x**2 + 10*np.sin(x)et on l'affiche :
>>> x = np.arange(-10, 10, 0.1)
>>> plt.plot(x, f(x))
>>> plt.show()Cette fonction possède un minimum global autour de -1.3 et un minimum local autour de 3.8.
La manière la plus commune et performante pour trouver un minimum de cette fonction est de réaliser une descente de gradient en commençant à partir d'un point initial donné. L'algorithme BFGS est une bonne façon pour réaliser cela :
>>> optimize.fmin_bfgs(f, 0)
Optimization terminated successfully.
Current function value: -7.945823
Iterations: 5
Function evaluations: 24
Gradient evaluations: 8
array([-1.30644003])Toutefois, avec cette approche, on peut se retrouver face à un problème. Si la fonction possède des minimums locaux, l'algorithme peut très bien trouver ces minimums locaux à la place du minimum global en fonction du point initial donné :
>>> optimize.fmin_bfgs(f, 3, disp=0)
array([ 3.83746663])Si nous ne connaissons pas le voisinage du minimum global afin de choisir un point initial cohérent, nous aurons besoin de recourir à une optimisation globale plus coûteuse en temps de calcul. Pour trouver le minimum global, l'algorithme le plus simple est le « brute force », la fonction est ainsi évaluée en chaque point de la grille donnée :
>>> grid = (-10, 10, 0.1)
>>> xmin_global = optimize.brute(f, (grid,))
>>> xmin_global
array([-1.30641113])Pour des grilles de tailles plus importantes, scipy.optimize.brute()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.brute.html#scipy.optimize.brute devient assez lent. scipy.optimize.anneal()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.anneal.html#scipy.optimize.anneal propose une alternative utilisant le « recuit simulé » (simulated annealing). Des algorithmes plus performants existent pour différents types de problèmes d'optimisation globale, mais cela est hors du cadre de cette présentation du module SciPy. Néanmoins, voici quelques librairies utiles consacrées à l'optimisation globale : OpenOpthttp://openopt.org/Welcome, IPOPThttps://github.com/xuy/pyipopt, PyGMOhttp://pagmo.sourceforge.net/pygmo/index.html et PyEvolvehttp://pyevolve.sourceforge.net/.
Afin de trouver le minimum local de la fonction, on peut aussi contraindre le domaine d'étude dans l'intervalle (0, 10) en utilisant scipy.optimize.fminbound()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fminbound.html#scipy.optimize.fminbound :
>>> xmin_local = optimize.fminbound(f, 0, 10)
>>> xmin_local
3.8374671...Vous trouverez une discussion plus détaillée traitant de la recherche des minimums d'une fonction dans le chapitre : Mathematical optimization: finding minima of functionshttp://scipy-lectures.github.io/advanced/mathematical_optimization/index.html#mathematical-optimization.
Rechercher les racines d'une fonction scalaire
Afin de trouver une racine de la fonction f ci-dessous, c.-à-d. un point où f(x)=0, nous pouvons utiliser par exemple la fonction scipy.optimize.fsolve()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fsolve.html#scipy.optimize.fsolve :
>>> root = optimize.fsolve(f, 1) # our initial guess is 1
>>> root
array([ 0.])Notez qu'ici, une seule racine a été trouvée. En inspectant le graphe de f, on remarque qu'il y a une autre racine autour de -2.5. Nous retrouvons la valeur exacte de cette racine en ajustant notre estimation initiale :
>>> root2 = optimize.fsolve(f, -2.5)
>>> root2
array([-2.47948183])Approximation de courbes
Supposons que nous ayons des données échantillonnées de la fonction f auxquelles nous ajoutons un bruit.
>>> xdata = np.linspace(-10, 10, num=20)
>>> ydata = f(xdata) + np.random.randn(xdata.size)À présent, si nous connaissons la fonction à partir de laquelle les échantillons ont été tirés (x^2 + sin(x) dans ce cas), mais pas les amplitudes associées, nous pouvons toutefois les trouver en approchant la courbe par la méthode des moindres carrés. Pour commencer, nous devons définir la fonction à approximer :
>>> def f2(x, a, b):
... return a*x**2 + b*np.sin(x)Ensuite, nous allons utiliser scipy.optimize.curve_fit()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html#scipy.optimize.curve_fit pour trouver a et b :
>>> guess = [2, 2]
>>> params, params_covariance = optimize.curve_fit(f2, xdata, ydata, guess)
>>> params
array([ 0.99925147, 9.76065551])Maintenant que nous avons trouvé les minimums et les racines de f et que nous avons utilisé l'approximation de courbe sur f, nous allons mettre tous les résultats ensemble sur le même graphe :
Dans SciPy 0.11 et les versions ultérieures, toutes les méthodes de minimisation et les algorithmes de recherches des racines ont été réunis dans une même interface, par exemple : scipy.optimize.minimize()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize, scipy.optimize.minimize_scalar()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize_scalar.html#scipy.optimize.minimize_scalar et scipy.optimize.root()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.root.html#scipy.optimize.root.
Cela permet de comparer facilement les algorithmes entre eux simplement en faisant varier les noms des méthodes.
Vous trouverez les algorithmes avec les mêmes fonctionnalités pour le cas multidimensionnel dans scipy.optimizehttp://docs.scipy.org/doc/scipy/reference/optimize.html#scipy.optimize.
Exercice : approximation de courbes et données de température
Les températures extrêmes en Alaska de chaque mois, en commençant par janvier, sont les suivantes (en degré Celcius) :
- max : 17, 19, 21, 28, 33, 38, 37, 37, 31, 23, 19, 18 ;
- min : -62, -59, -56, -46, -32, -18, -9, -13, -25, -46, -52, -58.
- Tracer ces températures extrêmes.
- Définir une fonction qui décrit les températures min et max. Astuces : cette fonction doit avoir une période de 1 an. Inclure un décalage de temps.
- Approcher cette fonction à partir des données avec scipy.optimize.curve_fit()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html#scipy.optimize.curve_fit.
- Tracer le résultat. Est-ce que l'approximation vous parait valable ? Sinon, pour quelles raisons ?
- Est-ce que le décalage de temps est le même pour les températures min et max et cela en accord avec la précision de l'approximation ?
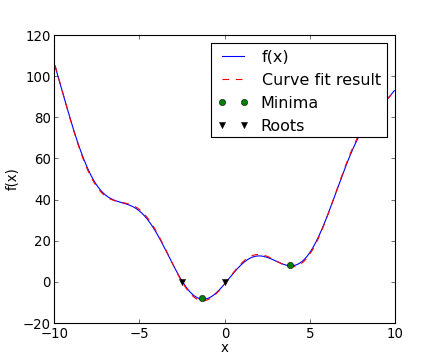
Exercice : minimisation 2D
La fonction « dos de chameau à six bosses »
a de multiples minimums : globaux et locaux. Trouver le minimum global de cette fonction.
Astuces :
- les variables peuvent être limitées à l'intervalle -2 < x < 2 et -1 < y < 1 ;
- utilisez numpy.meshgrid()http://docs.scipy.org/doc/numpy/reference/generated/numpy.meshgrid.html#numpy.meshgrid et pylab.imshow() pour déterminer visuellement les régions ;
- utilisez scipy.optimize.fmin_bfgs()http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fmin_bfgs.html#scipy.optimize.fmin_bfgs ou une autre méthode de minimisation multidimensionnelle.
Combien y a-t-il de minimums globaux, et quelle est la valeur de la fonction en ces points ? Que se passe-t-il lorsque la condition initiale est (x, y) = (0, 0) ?
Si vous souhaitez voir un exemple plus avancé, consultez l'exercice sur l'approximation de courbes par la méthode des moindres carrés : application pour extraire des points de mesure sur des données topographiques LiDAR.http://scipy-lectures.github.io/intro/summary-exercises/optimize-fit.html#summary-exercise-optimize
VII. Statistiques et nombres aléatoires : scipy.stats▲
Le module scipy.statshttp://docs.scipy.org/doc/scipy/reference/stats.html#scipy.stats contient des outils statistiques et des descriptions probabilistes sur les nombres aléatoires. Les générateurs de nombres aléatoires de nombreux processus aléatoires sont disponibles dans numpy.random.
VII-A. Histogramme et fonction de densité de probabilité▲
Les observations d'un processus aléatoire peuvent être décrites par leur histogramme qui est un estimateur de la densité de probabilité PDF (probability density function) du process aléatoire :
>>> a = np.random.normal(size=1000)
>>> bins = np.arange(-4, 5)
>>> bins
array([-4, -3, -2, -1, 0, 1, 2, 3, 4])
>>> histogram = np.histogram(a, bins=bins, normed=True)[0]
>>> bins = 0.5*(bins[1:] + bins[:-1])
>>> bins
array([-3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5])
>>> from scipy import stats
>>> b = stats.norm.pdf(bins) # norm is a distributionIn [1]: pl.plot(bins, histogram)
In [2]: pl.plot(bins, b)Si on connaît le processus aléatoire tel que le processus normal (gaussien), on peut réaliser une approximation par maximum de vraisemblance des observations pour estimer les paramètres de la distribution sous-jacente du processus aléatoire. Dans cet exemple, on réalise une approximation des données observées par un processus normal (gaussien) :
>>> loc, std = stats.norm.fit(a)
>>> loc
-0.045256707490...
>>> std
0.9870331586690...Exercice : distributions de probabilité
Générez 1000 nombres aléatoires à partir d'une distribution gamma avec un paramètre de forme égal à 1, puis tracez l'histogramme à partir de cet échantillon de données. Pouvez-vous tracer la PDF par-dessus (cela devrait correspondre, n'est-ce pas ?)
Supplément : les distributions possèdent de nombreuses méthodes utiles. Examinez-les en lisant la docstring (commentaire dans le code) ou en utilisant la complétion IPython. Pouvez-vous retrouver le paramètre de forme = 1 en utilisant la méthode d'approximation fit sur votre jeu d'essai ?
VII-B. Centiles (Percentiles en anglais souvent utilisé abusivement en français)▲
La médiane est la valeur qui permet de partager une série de données observées en deux parties possédant le même nombre d'éléments :
>>> np.median(a)
-0.058028034...Elle est également appelée le « centile 50 », car 50 % des observations sont situées au-dessus de cette valeur :
>>> stats.scoreatpercentile(a, 50)
-0.0580280347...De manière similaire, on peut calculer le « centile 90 » :
>>> stats.scoreatpercentile(a, 90)
1.231593551...Le centile est un estimateur de la fonction de distribution cumulée CDF (Cumulative Distribution Function).
VII-C. Tests statistiques▲
Un test statistique est un indicateur décisionnel. Par exemple, si nous avons deux jeux d'observations que nous affirmons qu'ils proviennent tous deux d'un processus gaussien, on peut utiliser un T-test pour décider si les deux jeux d'observations sont significativement différents ou pas :
>>> a = np.random.normal(0, 1, size=100)
>>> b = np.random.normal(1, 1, size=10)
>>> stats.ttest_ind(a, b)
(-3.75832707..., 0.00027786...)Le résultat de la fonction est composé de :
- la valeur statistique du T-test : il s'agit d'un nombre signé qui est proportionnel à la différence entre les deux processus aléatoires et qui possède une magnitude relative à cette différence ;
- la « p-valeur » : c'est la probabilité que les deux processus soient identiques. Proche de 1, les deux processus sont quasiment et très certainement identiques. Proche de zéro, cela signifie qu'ils n'ont pratiquement rien à voir entre eux et qu'ils décrivent deux tendances bien différentes.
VIII. Interpolation : scipy.interpolate▲
Le module scipy.interpolatehttp://docs.scipy.org/doc/scipy/reference/interpolate.html#scipy.interpolate est pratique pour approximer une fonction à partir de données expérimentales et donc d'évaluer les points où il n'existe pas de mesure réelle. Ce module est basé sur la routine FITPACK Fortranhttp://www.netlib.org/dierckx/index.html du projet netlib.
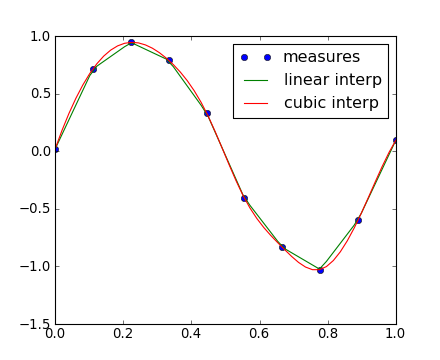
Imaginons des données expérimentales proches de la fonction sinus :
>>> measured_time = np.linspace(0, 1, 10)
>>> noise = (np.random.random(10)*2 - 1) * 1e-1
>>> measures = np.sin(2 * np.pi * measured_time) + noiseLa classe scipy.interpolate.interp1dhttp://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.interp1d.html#scipy.interpolate.interp1d permet de construire une fonction d'interpolation linéaire :
>>> from scipy.interpolate import interp1d
>>> linear_interp = interp1d(measured_time, measures)L'instance scipy.interpolate.linear_interp a ensuite besoin d'être évaluée dans l'intervalle de temps considéré :
>>> computed_time = np.linspace(0, 1, 50)
>>> linear_results = linear_interp(computed_time)On peut également réaliser une interpolation cubique à l'aide de mots-clés passés en argument :
>>> cubic_interp = interp1d(measured_time, measures, kind='cubic')
>>> cubic_results = cubic_interp(computed_time)L'ensemble de ces résultats est visible sur la figure Matplotlib suivante :
scipy.interpolate.interp2dhttp://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.interp2d.html#scipy.interpolate.interp2d est l'équivalent au module scipy.interpolate.interp1dhttp://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.interp1d.html#scipy.interpolate.interp1d pour les données en 2D. Pour les interpolations, le domaine calculé (interpolé) doit rester dans le domaine mesuré. Voir l'exercice sur la Prédiction de la vitesse maximale du venthttp://scipy-lectures.github.io/intro/summary-exercises/stats-interpolate.html#summary-exercise-stat-interp de la station de Sprogø pour avoir un exemple sur la méthode d'interpolation Spline (le mot anglais reste d'usage !)
IX. Intégration numérique : scipy.integrate▲
La routine d'intégration la plus commune est scipy.integrate.quad()http://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.quad.html#scipy.integrate.quad :
>>> from scipy.integrate import quad
>>> res, err = quad(np.sin, 0, np.pi/2)
>>> np.allclose(res, 1)
True
>>> np.allclose(err, 1 - res)
TrueD'autres schémas d'intégration sont disponibles comme fixed_quad, quadrature, romberg.
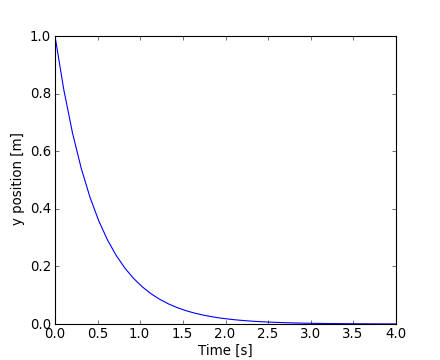
Le module scipy.integratehttp://docs.scipy.org/doc/scipy/reference/integrate.html#scipy.integrate propose également des routines pour intégrer des Équations Différentielles Ordinaires (ODE en anglais). En particulier, scipy.integrate.odeint()http://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html#scipy.integrate.odeint qui permet de réaliser des intégrations en utilisant la méthode LSODA (Livermore Solver for Ordinary Differential equations avec un aiguillage automatique pour résoudre soit des équations différentielles dites « raides », soit « non raides »).
scipy.integrate.odeint() résout des systèmes d'ODE de la forme :
dy/dt = rhs(y1, y2, .., t0,...)Par exemple, essayons de résoudre l'ODE dy/dt = -2y dans l'intervalle t = 0..4 avec une condition initiale y(t=0) = 1. En premier lieu, la fonction dérivée dy/dt (variation de y en fonction du temps) doit être définie :
>>> def calc_derivative(ypos, time, counter_arr):
... counter_arr += 1
... return -2 * ypos
...Une variable supplémentaire counter_arr a été ajoutée pour montrer que la fonction peut être appelée plusieurs fois de suite dans le même pas de temps, et cela, jusqu'à la convergence de la solution.
Le compteur (c'est un tableau) est défini ainsi :
>>> counter = np.zeros((1,), dtype=np.uint16)La trajectoire sera calculée de la manière suivante :
>>> from scipy.integrate import odeint
>>> time_vec = np.linspace(0, 4, 40)
>>> yvec, info = odeint(calc_derivative, 1, time_vec,
... args=(counter,), full_output=True)Par conséquent, la fonction dérivée a été appelée plus de 40 fois (ce qui était initialement le nombre de pas de temps) :
>>> counter
array([129], dtype=uint16)Le nombre cumulé d'itérations pour chacun des 10 premiers pas de temps peut être obtenu par :
>>> info['nfe'][:10]
array([31, 35, 43, 49, 53, 57, 59, 63, 65, 69], dtype=int32)À noter que la méthode de résolution a besoin de plus d'itérations lors du premier pas de temps. La solution yvec pour la trajectoire est tracée ci-dessous :
Un autre exemple d'utilisation de scipy.integrate.odeint()http://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html#scipy.integrate.odeint pourrait être celui d'un oscillateur harmonique, c.-à-d. oscillateur masse-ressort (oscillateur du 2d ordre). La position d'une masse suspendue à un ressort obéit à une ODE du 2d degré du type : y'' + 2 eps wo y' + wo^2 y = 0 avec wo^2 = k/m, k représentant la constante de raideur du ressort, m la masse et eps=c/(2 m wo) avec c le coefficient d'amortissement du fluide environnant. Pour cet exemple, nous avons choisi les paramètres suivants :
>>> mass = 0.5 # kg
>>> kspring = 4 # N/m
>>> cviscous = 0.4 # N s/mAvec ces constantes, le système oscillant sera amorti peu à peu jusqu'à l'équilibre à cause de :
>>> eps = cviscous / (2 * mass * np.sqrt(kspring/mass))
>>> eps < 1
TrueAvec la méthode de résolution scipy.integrate.odeint()http://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html#scipy.integrate.odeint, l'équation du 2d degré doit être transformée en un système de deux équations du 1er degré avec le vecteur Y=(y, y').
Il sera alors pratique de définir nu = 2 eps * wo = c / m et om = wo^2 = k/m :
>>> nu_coef = cviscous / mass
>>> om_coef = kspring / massLa fonction suivante va calculer la vitesse et l'accélération ainsi :
>>> def calc_deri(yvec, time, nuc, omc):
... return (yvec[1], -nuc * yvec[1] - omc * yvec[0])
...
>>> time_vec = np.linspace(0, 10, 100)
>>> yarr = odeint(calc_deri, (1, 0), time_vec, args=(nu_coef, om_coef))La position finale du ressort et la vitesse d'oscillation sont visibles sur la figure Matplotlib suivante :
N. B. Il n'y a pas de méthode de résolution d'équations différentielles partielles (PDE) dans le module SciPy. Plusieurs librairies Python sont disponibles pour résoudre les PDE, tels que fipyhttp://www.ctcms.nist.gov/fipy/ ou SfePyhttp://code.google.com/p/sfepy/.
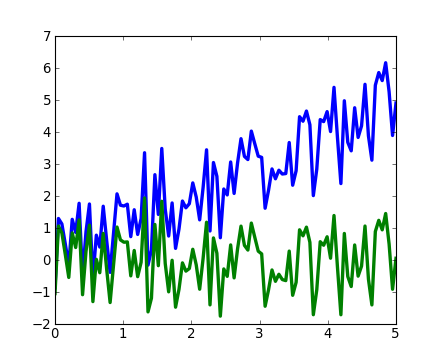
X. Traitement du signal : scipy.signal▲
>>> from scipy import signalscipy.signal.detrend()http://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.detrend.html#scipy.signal.detrend supprime les composantes linéaires du signal :
t = np.linspace(0, 5, 100)
x = t + np.random.normal(size=100)
pl.plot(t, x, linewidth=3)
pl.plot(t, signal.detrend(x), linewidth=3)scipy.signal.resample()http://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.resample.html#scipy.signal.resample, ré-échantillonnage du signal en n points à l'aide de la FFT.
t = np.linspace(0, 5, 100)
x = np.sin(t)
pl.plot(t, x, linewidth=3)
pl.plot(t[::2], signal.resample(x, 50), 'ko')scipy.signalhttp://docs.scipy.org/doc/scipy/reference/signal.html#scipy.signal possède beaucoup de fonctions de fenêtrage comme scipy.signal.hamming()http://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.hamming.html#scipy.signal.hamming, scipy.signal.bartlett()http://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.bartlett.html#scipy.signal.bartlett, scipy.signal.blackman()http://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.blackman.html#scipy.signal.blackman…
scipy.signalhttp://docs.scipy.org/doc/scipy/reference/signal.html#scipy.signal possède également des fonctions filtres (filtre médian scipy.signal.medfilt()http://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.medfilt.html#scipy.signal.medfilt, filtre Wiener scipy.signal.wiener()http://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.wiener.html#scipy.signal.wiener). Ces fonctions filtres seront décrites dans le chapitre consacré au traitement d'images plus loin.
XI. Traitement d'images : scipy.ndimage▲
Le sous-module consacré au traitement d'images dans SciPy est scipy.ndimagehttp://docs.scipy.org/doc/scipy/reference/ndimage.html#scipy.ndimage.
>>> from scipy import ndimageLes routines de traitement d'images sont classées par catégorie de traitement qu'elles réalisent.
XI-A. Transformations géométriques sur les images▲
Pour modifier l'orientation, la résolution…
>>> from scipy import misc
>>> lena = misc.lena()
>>> shifted_lena = ndimage.shift(lena, (50, 50))
>>> shifted_lena2 = ndimage.shift(lena, (50, 50), mode='nearest')
>>> rotated_lena = ndimage.rotate(lena, 30)
>>> cropped_lena = lena[50:-50, 50:-50]
>>> zoomed_lena = ndimage.zoom(lena, 2)
>>> zoomed_lena.shape
(1024, 1024)XI-B. Filtrage d'images▲
>>> from scipy import misc
>>> lena = misc.lena()
>>> import numpy as np
>>> noisy_lena = np.copy(lena).astype(np.float)
>>> noisy_lena += lena.std()*0.5*np.random.standard_normal(lena.shape)
>>> blurred_lena = ndimage.gaussian_filter(noisy_lena, sigma=3)
>>> median_lena = ndimage.median_filter(blurred_lena, size=5)
>>> from scipy import signal
>>> wiener_lena = signal.wiener(blurred_lena, (5,5))De nombreux autres filtres peuvent être appliqués aux images et sont disponibles dans scipy.ndimage.filtershttp://docs.scipy.org/doc/scipy/reference/ndimage.html#scipy.ndimage.filters et scipy.signalhttp://docs.scipy.org/doc/scipy/reference/signal.html#scipy.signal.
Exercice
Comparez les histogrammes sur une image filtrée par différents filtres.
XI-C. Morphologie mathématique▲
La morphologie en mathématique est une théorie mathématique qui découle d'une série de théories. Elle permet de caractériser et de transformer des structures géométriques. Les images binaires (noir et blanc) en particulier, peuvent être transformées en utilisant cette théorie : la série de pixels à transformer correspond à celle des pixels de valeur non nulle au voisinage de cette série. La théorie s'étend également aux images en niveau de gris.
Les opérations élémentaires de morphologie en mathématique utilisent une « structure » (structuring element) afin de modifier d'autres structures géométriques.
Pour commencer, générons une structure élémentaire :
>>> el = ndimage.generate_binary_structure(2, 1)
>>> el
array([[False, True, False],
[True, True, True],
[False, True, False]], dtype=bool)
>>> el.astype(np.int)
array([[0, 1, 0],
[1, 1, 1],
[0, 1, 0]])Érosion
>>> a = np.zeros((7,7), dtype=np.int)
>>> a[1:6, 2:5] = 1
>>> a
array([[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0]])
>>> ndimage.binary_erosion(a).astype(a.dtype)
array([[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]])
>>> #Erosion removes objects smaller than the structure
>>> ndimage.binary_erosion(a, structure=np.ones((5,5))).astype(a.dtype)
array([[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]])Dilatation
>>> a = np.zeros((5, 5))
>>> a[2, 2] = 1
>>> a
array([[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]])
>>> ndimage.binary_dilation(a).astype(a.dtype)
array([[ 0., 0., 0., 0., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 1., 1., 1., 0.],
[ 0., 0., 1., 0., 0.],
[ 0., 0., 0., 0., 0.]])Ouverture
>>> a = np.zeros((5,5), dtype=np.int)
>>> a[1:4, 1:4] = 1; a[4, 4] = 1
>>> a
array([[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 1]])
>>> # Opening removes small objects
>>> ndimage.binary_opening(a, structure=np.ones((3,3))).astype(np.int)
array([[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 0, 0]])
>>> # Opening can also smooth corners
>>> ndimage.binary_opening(a).astype(np.int)
array([[0, 0, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 0, 0]])Fermeture : ndimage.binary_closing
Exercice
Vérifier que l'ouverture correspond à l'érosion puis à la dilatation.
Une opération d'ouverture supprime les petites structures de l'image, alors que l'opération de fermeture va remplir les petits trous. De telles opérations peuvent donc être utilisées pour « nettoyer » une image.
>>> a = np.zeros((50, 50))
>>> a[10:-10, 10:-10] = 1
>>> a += 0.25*np.random.standard_normal(a.shape)
>>> mask = a>=0.5
>>> opened_mask = ndimage.binary_opening(mask)
>>> closed_mask = ndimage.binary_closing(opened_mask)Exercice
Vérifier que la surface du carré reconstruit est plus petite que la surface du carré original.
(Le contraire serait arrivé si nous avions utilisé l'opération de fermeture avant celle d'ouverture).
Pour les images en niveau de gris, l'érosion (respectivement la dilatation) se traduit par le remplacement d'un pixel par la valeur minimale (respectivement maximale) parmi les pixels couverts par la structure élémentaire centrée en ce pixel.
>>> a = np.zeros((7,7), dtype=np.int)
>>> a[1:6, 1:6] = 3
>>> a[4,4] = 2; a[2,3] = 1
>>> a
array([[0, 0, 0, 0, 0, 0, 0],
[0, 3, 3, 3, 3, 3, 0],
[0, 3, 3, 1, 3, 3, 0],
[0, 3, 3, 3, 3, 3, 0],
[0, 3, 3, 3, 2, 3, 0],
[0, 3, 3, 3, 3, 3, 0],
[0, 0, 0, 0, 0, 0, 0]])
>>> ndimage.grey_erosion(a, size=(3,3))
array([[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 1, 1, 1, 0, 0],
[0, 0, 3, 2, 2, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]])XI-D. Mesures sur les images▲
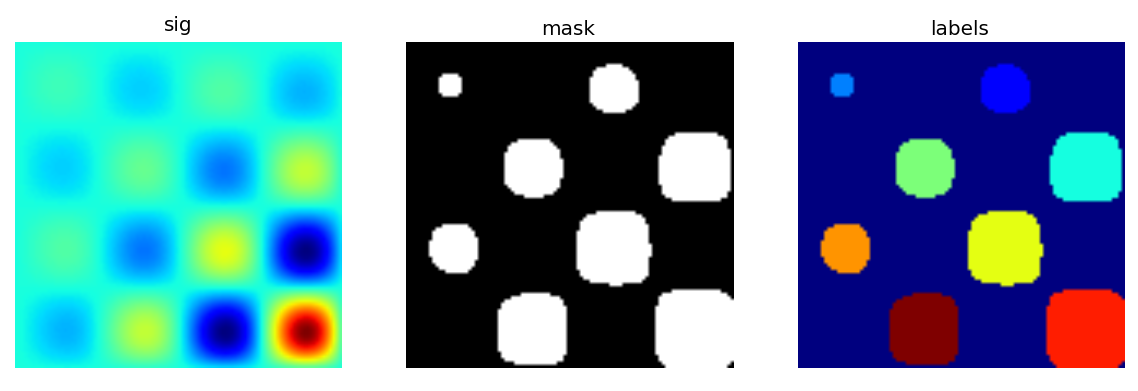
Commençons par générer une jolie image de synthèse binaire.
>>> x, y = np.indices((100, 100))
>>> sig = np.sin(2*np.pi*x/50.)*np.sin(2*np.pi*y/50.)*(1+x*y/50.**2)**2
>>> mask = sig > 1À présent, recherchons quelques informations sur l'image :
>>> labels, nb = ndimage.label(mask)
>>> nb
8
>>> areas = ndimage.sum(mask, labels, xrange(1, labels.max()+1))
>>> areas
array([ 190., 45., 424., 278., 459., 190., 549., 424.])
>>> maxima = ndimage.maximum(sig, labels, xrange(1, labels.max()+1))
>>> maxima
array([ 1.80238238, 1.13527605, 5.51954079, 2.49611818,
6.71673619, 1.80238238, 16.76547217, 5.51954079])
>>> ndimage.find_objects(labels==4)
[(slice(30L, 48L, None), slice(30L, 48L, None))]
>>> sl = ndimage.find_objects(labels==4)
>>> import pylab as pl
>>> pl.imshow(sig[sl[0]])
<matplotlib.image.AxesImage object at ...>Pour en savoir plus, voir l'exercice d'application en traitement d'images : comptage de bulles et de grains.
XII. Exercices de Calculs Scientifiques▲
Les exercices suivants utilisent principalement NumPy, SciPy et Matplotlib. Ils proposent quelques exemples concrets de calculs scientifiques exécutés avec Python. Maintenant que vous vous êtes familiarisé avec NumPy et SciPy, nous vous invitons à les tester.
Exercices
- Prédiction de la vitesse maximale du vent de la station de Sprogø.
- Approximation de courbes non linéaires par la méthode des moindres carrés : application pour extraire des points de mesure sur des données topographiques LiDAR.
- Application en traitement d'images : comptage de bulles et de grains.
- Exemple de solution pour l'exercice de traitement d'images : comptage de grains dans un verre.
XIII. Remerciements ▲
Merci aux personnes suivantes pour leur aide durant la traduction :
Retrouvez Les notes de cours scientifiques de Python.