I. Les tableaux NumPy▲
I-A. Présentation de NumPy et de ses tableaux▲
I-A-1. Les tableaux NumPy▲
|
Objets Python |
|
|
Apports de NumPy |
|
>>> import numpy as np
>>> a = np.array([0, 1, 2, 3])
>>> a
array([0, 1, 2, 3])Par exemple, un tableau contenant :
- des valeurs expérimentales ou issues d'une simulation numérique à intervalles de temps réguliers ;
- des enregistrements de signaux effectués via un équipement dédié comme un micro ;
- les pixels d'une image, en niveaux de gris ou en couleur ;
- des données 3D correspondant à des coordonnées X-Y-Z, telle une image issue d'un scanner IRM (Imagerie à Résonance Magnétique).
- …
Pourquoi est-ce utile ? Le tableau NumPy est un conteneur permettant l'optimisation de la mémoire afin de garantir une grande rapidité de calcul.
In [1]: L = range(1000)
In [2]: %timeit [i**2 for i in L]
1000 loops, best of 3: 403 us per loop
In [3]: a = np.arange(1000)
In [4]: %timeit a**2
100000 loops, best of 3: 12.7 us per loopI-A-2. La documentation de référence de NumPy▲
- Sur le web : http://docs.scipy.org/http://docs.scipy.org/
-
Aide interactive :
SélectionnezIn [5]: np.array? String Form:<built-infunction array>Docstring:array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0, ... - Faire une recherche par mot-clé :
>>> np.lookfor('create array')
Search results for 'create array'
---------------------------------
numpy.array
Create an array.
numpy.memmap
Create a memory-map to an array stored in a *binary* file on disk.In [6]: np.con*?
np.concatenate
np.conj
np.conjugate
np.convolveI-A-3. Les conventions d'import▲
La méthode recommandée pour importer NumPy est la suivante :
>>> import numpy as npI-B. Créer des tableaux▲
I-B-1. Construction manuelle de tableaux▲
- Tableau unidimensionnel (1D)
>>> a = np.array([0, 1, 2, 3])
>>> a
array([0, 1, 2, 3])
>>> a.ndim
1
>>> a.shape
(4,)
>>> len(a)
4- Tableau multidimensionnel (2D, 3D…)
>>> b = np.array([[0, 1, 2], [3, 4, 5]]) # 2 x 3 array
>>> b
array([[0, 1, 2],
[3, 4, 5]])
>>> b.ndim
2
>>> b.shape
(2, 3)
>>> len(b) # returns the size of the first dimension
2
>>> c = np.array([[[1], [2]], [[3], [4]]])
>>> c
array([[[1],
[2]],
[[3],
[4]]])
>>> c.shape
(2, 2, 1)Exercice : tableaux simples
- Créez un simple tableau 2D. Pour commencer, refaites les exemples ci-dessus. Puis créez le vôtre : combien de nombres impairs sur la première ligne en les comptant à partir de la fin, et de nombres pairs sur la seconde ?
- Utilisez les fonctions len
() et numpy.shape() sur ces tableaux. Quelle est la relation entre ces deux fonctions ? Et que retourne l'attribut ndim de chacun de ces tableaux ?
I-B-2. Fonctions pour créer des tableaux▲
Dans la pratique, on ne saisit que rarement les éléments un à un.
-
Création d'un tableau de valeurs uniformément espacées
Sélectionnez>>>a=np.arange(10)# 0 .. n-1 (!)>>>aarray([0,1,2,3,4,5,6,7,8,9])>>>b=np.arange(1,9,2)# start, end (exclusive), step>>>barray([1,3,5,7]) -
Similaire à arange, mais en précisant le nombre de points au lieu du pas
Sélectionnez>>>c=np.linspace(0,1,6)# start, end, num-points>>>carray([0.,0.2,0.4,0.6,0.8,1.])>>>d=np.linspace(0,1,5, endpoint=False)>>>darray([0.,0.2,0.4,0.6,0.8]) -
Tableaux courants
Sélectionnez>>>a=np.ones((3,3))# reminder: (3, 3) is a tuple>>>aarray([[1.,1.,1.], [1.,1.,1.], [1.,1.,1.]])>>>b=np.zeros((2,2))>>>barray([[0.,0.], [0.,0.]])>>>c=np.eye(3)>>>carray([[1.,0.,0.], [0.,1.,0.], [0.,0.,1.]])>>>d=np.diag(np.array([1,2,3,4]))>>>darray([[1,0,0,0], [0,2,0,0], [0,0,3,0], [0,0,0,4]]) - np.random : nombres aléatoires
>>> a = np.random.rand(4) # uniform in [0, 1]
>>> a
array([ 0.95799151, 0.14222247, 0.08777354, 0.51887998])
>>> b = np.random.randn(4) # Gaussian
>>> b
array([ 0.37544699, -0.11425369, -0.47616538, 1.79664113])
>>> np.random.seed(1234) # Setting the random seedExercice : créer des tableaux en utilisant des fonctions
- Expérimentez avec arange, linspace, ones, zeros, eye et diag.
- Créez différents types de tableaux avec des nombres aléatoires.
- Essayez en initialisant la valeur de la graine aléatoire (random seed) avant de créer le tableau avec des valeurs aléatoires.
- Regardez la fonction np.empty. Que fait-elle ? Quand peut-elle être utile ?
I-C. Les différents types de données basiques▲
Vous avez peut-être remarqué que dans certains cas, les éléments d'un tableau sont affichés au format float (2. au lieu de 2). Cela est dû à la gestion du type de données :
>>> a = np.array([1, 2, 3])
>>> a.dtype
dtype('int64')
>>> b = np.array([1., 2., 3.])
>>> b.dtype
dtype('float64')Les différents types de données existants nous permettent de mieux gérer l'occupation mémoire des données, mais la plupart du temps, nous travaillerons simplement avec des nombres à virgule flottante. Veuillez noter que dans l'exemple ci-dessus, NumPy détecte automatiquement le type de données en entrée.
Vous pouvez explicitement spécifier le type à utiliser :
>>> c = np.array([1, 2, 3], dtype=float)
>>> c.dtype
dtype('float64')Par défaut, le type utilisé est le float :
>>> a = np.ones((3, 3))
>>> a.dtype
dtype('float64')Mais il existe d'autres types :
|
Nombres complexes : |
Sélectionnez |
|
Booléens : |
Sélectionnez |
|
Chaînes de caractères : |
Sélectionnez |
|
Mais aussi : |
|
I-D. Visualisation basique▲
Maintenant que nous avons nos premiers tableaux de données, nous allons visualiser leur contenu.
Commençons par lancer IPython en mode pylab.
$ ipython --pylabOu le notebook :
$ ipython notebook --pylab=inlineSinon, si IPython est déjà lancé :
>>> %pylabOu, depuis le notebook :
>>> %pylab inlineLe inline est important dans le notebook, car il permet l'affichage dans le notebook même et non dans une nouvelle fenêtre.
Matplotlib est un outil de tracés de graphiques 2D. Nous pouvons importer ses fonctions ainsi :
>>> import matplotlib.pyplot as plt # the tidy wayPuis on les utilise comme suit (notez que vous devez utiliser show de manière explicite) :
>>> plt.plot(x, y) # line plot
>>> plt.show() # <-- shows the plot (not needed with pylab)Ou encore, si vous utilisez pylab :
>>> plot(x, y) # line plotUtiliser import matplotlib.pyplot as plt est recommandé dans les scripts. Tandis que pylab est plus recommandé pour le travail interactif.
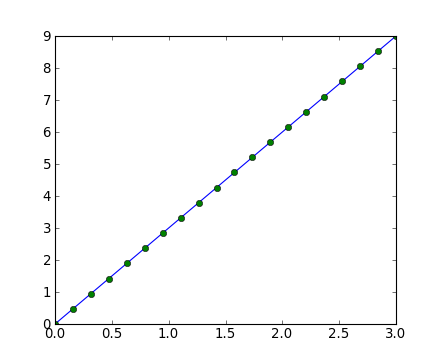
- Tracé de courbe 1D
>>> x = np.linspace(0, 3, 20)
>>> y = np.linspace(0, 9, 20)
>>> plt.plot(x, y) # line plot
[<matplotlib.lines.Line2D object at ...>]
>>> plt.plot(x, y, 'o') # dot plot
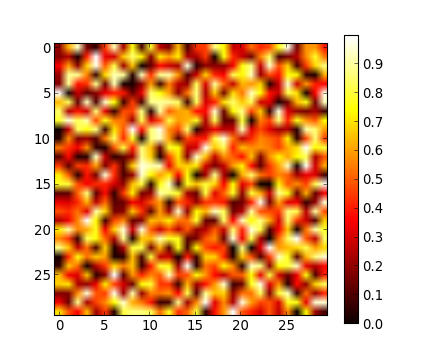
[<matplotlib.lines.Line2D object at ...>]- Tableaux 2D (par exemple, les pixels d'une image) :
>>> image = np.random.rand(30, 30)
>>> plt.imshow(image, cmap=plt.cm.hot)
>>> plt.colorbar()
<matplotlib.colorbar.Colorbar instance at ...>Exercice : visualisation basique
- Réalisez des graphiques à partir de tableaux simples : un cosinus en fonction du temps et une matrice 2D.
- Essayez d'utiliser la palette de couleurs gray dans une matrice 2D.
I-E. Indexation et échantillonnage▲
Les éléments d'un tableau peuvent être accédés et assignés de la même façon que les listes en Python :
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a[0], a[2], a[-1]
(0, 2, 9)Les indices commencent à 0, comme n'importe quelle séquence Python (ou C/C++). Au contraire, donc, du Fortran ou de Matlab, dont les indices commencent à 1.
L'idiome usuel de Python pour lire une séquence à l'envers est également supporté :
>>> a[::-1]
array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])Pour des tableaux multidimensionnels, les index sont des tuples d'entiers :
>>> a = np.diag(np.arange(3))
>>> a
array([[0, 0, 0],
[0, 1, 0],
[0, 0, 2]])
>>> a[1, 1]
1
>>> a[2, 1] = 10 # third line, second column
>>> a
array([[ 0, 0, 0],
[ 0, 1, 0],
[ 0, 10, 2]])
>>> a[1]
array([0, 1, 0])- En 2D, la première dimension correspond à la ligne, et la seconde à la colonne.
- Pour les tableaux multidimensionnels, a, a[0] sont interprétés comme demandant tous les éléments du tableau dans la ou les dimensions non spécifiées.
Échantillonnage (ou slicing) : les tableaux, comme toute séquence Python, peuvent être échantillonnés :
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a[2:9:3] # [start:end:step]
array([2, 5, 8])Notez que le dernier index n'est pas inclus :
>>> a[:4]
array([0, 1, 2, 3])Les trois arguments start, end et step du slicing ne sont pas forcément tous requis : par défaut, l'index de départ start vaut 0, l'index d'arrivée end est celui du dernier élément et le pas step vaut 1 :
>>> a[1:3]
array([1, 2])
>>> a[::2]
array([0, 2, 4, 6, 8])
>>> a[3:]
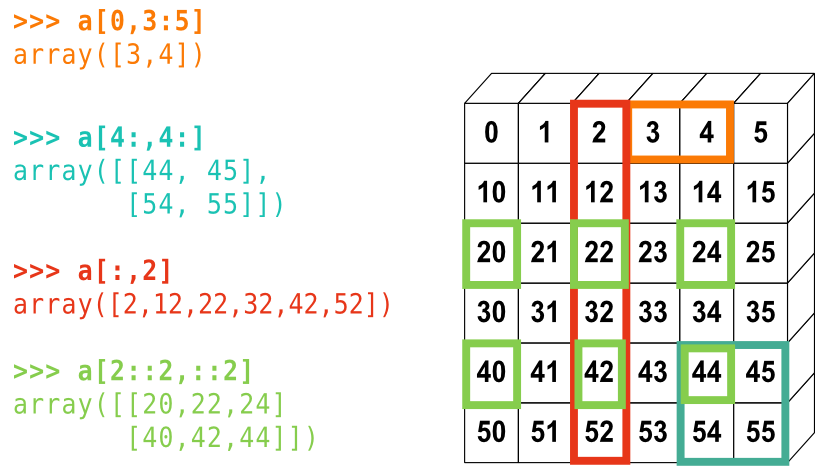
array([3, 4, 5, 6, 7, 8, 9])La petite illustration suivante résume bien la façon dont NumPy gère l'indexation et l'échantillonnage :
Vous pouvez également combiner les deux techniques :
>>> a = np.arange(10)
>>> a[5:] = 10
>>> a
array([ 0, 1, 2, 3, 4, 10, 10, 10, 10, 10])
>>> b = np.arange(5)
>>> a[5:] = b[::-1]
>>> a
array([0, 1, 2, 3, 4, 4, 3, 2, 1, 0])Exercice : indexation et échantillonnage
- Essayez les différentes possibilités de l'échantillonnage : en partant d'un linspace, essayez de récupérer les nombres impairs, en partant de la fin, puis les nombres pairs en partant du début.
- Reproduisez les différents échantillonnages du diagramme ci-dessus. Utilisez l'expression suivante pour créer le tableau de base :
>>> np.arange(6) + np.arange(0, 51, 10)[:, np.newaxis]
array([[ 0, 1, 2, 3, 4, 5],
[10, 11, 12, 13, 14, 15],
[20, 21, 22, 23, 24, 25],
[30, 31, 32, 33, 34, 35],
[40, 41, 42, 43, 44, 45],
[50, 51, 52, 53, 54, 55]])Exercice : création de tableaux
Créez les tableaux suivants (avec les mêmes données et types) :
[[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 2],
[1, 6, 1, 1]]
[[0., 0., 0., 0., 0.],
[2., 0., 0., 0., 0.],
[0., 3., 0., 0., 0.],
[0., 0., 4., 0., 0.],
[0., 0., 0., 5., 0.],
[0., 0., 0., 0., 6.]]Astuce : les éléments d'un tableau sont accessibles de la même manière qu'avec une liste (ex. : a[1] ou a[1, 2]).
Astuce : examinez la docstring de diag.
Exercice : création de tableaux par répétition
Fouillez la documentation pour trouver les informations concernant np.tile, et utilisez cette fonction pour construire le tableau suivant :
[[4, 3, 4, 3, 4, 3],
[2, 1, 2, 1, 2, 1],
[4, 3, 4, 3, 4, 3],
[2, 1, 2, 1, 2, 1]]I-F. Copie et visualisation▲
Toute opération d'échantillonnage crée une vue du tableau original, qui consiste juste en une façon différente d'accéder aux données du tableau. Aussi, ce tableau n'est pas recopié en mémoire. Vous pouvez utiliser np.may_share_memory() pour vérifier si deux tableaux partagent le même espace mémoire. Notez également que cela utilise des heuristiques et peut vous renvoyer de faux positifs.
Quand vous modifiez une vue, le tableau originel est également modifié :
>>> a = np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> b = a[::2]
>>> b
array([0, 2, 4, 6, 8])
>>> np.may_share_memory(a, b)
True
>>> b[0] = 12
>>> b
array([12, 2, 4, 6, 8])
>>> a # (!)
array([12, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a = np.arange(10)
>>> c = a[::2].copy() # force a copy
>>> c[0] = 12
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> np.may_share_memory(a, c)
FalseCela peut paraître surprenant de prime abord, mais cela permet de gagner en mémoire et en temps de traitement.
Exemple : filtre pour nombres premiers
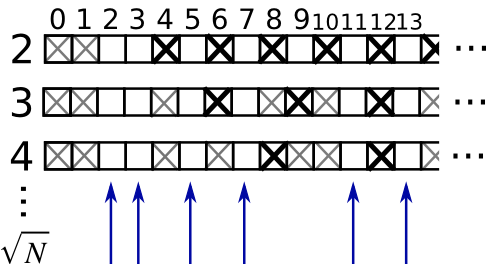
Calculer les nombres premiers entre 0 et 99, à l'aide d'un masque.
- Construisez un tableau booléen is_prime de type (100,), rempli avec True
>>> is_prime = np.ones((100,), dtype=bool)- Annotez à
False0 et 1 qui ne sont pas des nombres premiers :
>>> is_prime[:2] = 0- Pour chaque entier j à partir de 2, mettez à
Falsetous ses multiples :
>>> N_max = int(np.sqrt(len(is_prime)))
>>> for j in range(2, N_max):
... is_prime[2*j::j] = False- À l'aide de
help(no.nonzero), affichez les nombres premiers. -
Effectuez les tâches suivantes :
- placez les codes précédents dans un module et nommez-le prime_sieve.py ;
- lancez-le pour vous assurer qu'il fonctionne ;
-
implémentez la version optimisée du Crible d'Eratosthèneshttp://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
- ne tenez pas compte de j qui n'est pas un nombre premier,
- le premier nombre à supprimer est j2.
I-G. Indexation avancée▲
Les tableaux Numpy peuvent être indexés grâce à l'échantillonnage, mais aussi avec des tableaux de booléens ou d'entiers (masques). Cette méthode est appelée : indexation avancée (fancy indexing). Cela crée des copies et non des vues.
I-G-1. Utilisation de masque booléen▲
>>> np.random.seed(3)
>>> a = np.random.random_integers(0, 20, 15)
>>> a
array([10, 3, 8, 0, 19, 10, 11, 9, 10, 6, 0, 20, 12, 7, 14])
>>> (a % 3 == 0)
array([False, True, False, True, False, False, False, True, False,
True, True, False, True, False, False], dtype=bool)
>>> mask = (a % 3 == 0)
>>> extract_from_a = a[mask] # or, a[a%3==0]
>>> extract_from_a # extract a sub-array with the mask
array([ 3, 0, 9, 6, 0, 12])L'indexation via un masque peut être très utile pour assigner des valeurs à un tableau issues du premier.
>>> a[a % 3 == 0] = -1
>>> a
array([10, -1, 8, -1, 19, 10, 11, -1, 10, -1, -1, 20, -1, 7, 14])I-G-2. Indexation à l'aide d'un tableau d'entiers▲
>>> a = np.arange(0, 100, 10)
>>> a
array([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90])L'indexation peut être effectuée avec des tableaux d'entiers, où le même index est répété à plusieurs reprises :
>>> a[[2, 3, 2, 4, 2]] # note: [2, 3, 2, 4, 2] is a Python list
array([20, 30, 20, 40, 20])De nouvelles valeurs peuvent être assignées comme suit :
>>> a[[9, 7]] = -100
>>> a
array([ 0, 10, 20, 30, 40, 50, 60, -100, 80, -100])Quand un nouveau tableau est créé en indexant par l'intermédiaire d'un tableau d'entiers, le nouveau tableau a la même forme que le tableau d'origine :
>>> a = np.arange(10)
>>> idx = np.array([[3, 4], [9, 7]])
>>> idx.shape
(2, 2)
>>> a[idx]
array([[3, 4],
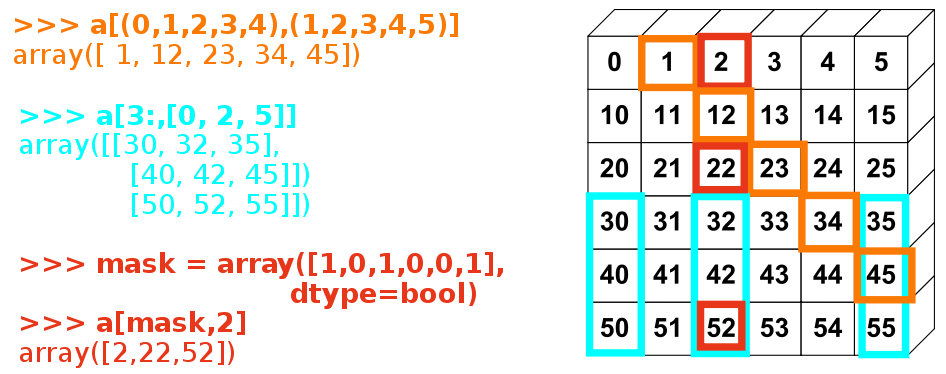
[9, 7]])L'image ci-dessous montre diverses utilisations d'indexations avancées :
Exercice : indexation avancée
Une fois de plus, reproduisez l'indexation avancée du diagramme ci-dessus.
Utilisez l'indexation avancée d'un côté et la création de tableaux de l'autre pour assigner les valeurs d'un tableau, par exemple en modifiant les éléments du tableau du diagramme qui sont en dessous de zéro.
II. Opérations numériques sur les tableaux NumPy▲
II-A. Opérations sur les éléments▲
II-A-1. Opérations basiques▲
Avec des scalaires :
>>> a = np.array([1, 2, 3, 4])
>>> a + 1
array([2, 3, 4, 5])
>>> 2**a
array([ 2, 4, 8, 16])Opérations élémentaires :
>>> b = np.ones(4) + 1
>>> a - b
array([-1., 0., 1., 2.])
>>> a * b
array([ 2., 4., 6., 8.])
>>> j = np.arange(5)
>>> 2**(j + 1) - j
array([ 2, 3, 6, 13, 28])Ces opérations sont, bien entendu, plus rapides que si vous les exécutiez directement en pur Python :
>>> a = np.arange(10000)
>>> %timeit a + 1
10000 loops, best of 3: 24.3 us per loop
>>> l = range(10000)
>>> %timeit [i+1 for i in l]
1000 loops, best of 3: 861 us per loopUne multiplication de tableaux n'est pas une multiplication de matrices
>>> c = np.ones((3, 3))
>>> c * c # NOT matrix multiplication!
array([[ 1., 1., 1.],
[ 1., 1., 1.],
[ 1., 1., 1.]])Multiplication de matrices
>>> c.dot(c)
array([[ 3., 3., 3.],
[ 3., 3., 3.],
[ 3., 3., 3.]])Exercice : opérations élémentaires
- Essayez des opérations arithmétiques basiques : addition des nombres pairs et impairs ;
- horodatez-les via %timeit ;
-
Générez :
- [2**0, 2**1, 2**2, 2**3, 2**4],
- a_j = 2^(3*j) – j.
II-A-2. Opérations complémentaires▲
Comparaisons :
>>> a = np.array([1, 2, 3, 4])
>>> b = np.array([4, 2, 2, 4])
>>> a == b
array([False, True, False, True], dtype=bool)
>>> a > b
array([False, False, True, False], dtype=bool)Comparaison de tableaux :
>>> a = np.array([1, 2, 3, 4])
>>> b = np.array([4, 2, 2, 4])
>>> c = np.array([1, 2, 3, 4])
>>> np.array_equal(a, b)
False
>>> np.array_equal(a, c)
TrueOpérations logiques :
>>> a = np.array([1, 1, 0, 0], dtype=bool)
>>> b = np.array([1, 0, 1, 0], dtype=bool)
>>> np.logical_or(a, b)
array([ True, True, True, False], dtype=bool)
>>> np.logical_and(a, b)
array([ True, False, False, False], dtype=bool)Fonctions transcendantales :
>>> a = np.arange(5)
>>> np.sin(a)
array([ 0. , 0.84147098, 0.90929743, 0.14112001, -0.7568025])
>>> np.log(a)
array([ -inf, 0. , 0.69314718, 1.09861229, 1.38629436])
>>> np.exp(a)
array([ 1.00000000e+00, 2.71828183e+00, 7.38905610e+00,
2.00855369e+01, 5.45981500e+01])Comparaisons de structure :
>>> a = np.arange(4)
>>> a + np.array([1, 2])
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (4) (2)broadcasting ? Nous y reviendrons plus tard.
Transpositions :
>>> a = np.triu(np.ones((3, 3)), 1) # see help(np.triu)
>>> a
array([[ 0., 1., 1.],
[ 0., 0., 1.],
[ 0., 0., 0.]])
>>> a.T
array([[ 0., 0., 0.],
[ 1., 0., 0.],
[ 1., 1., 0.]])La transposition est une vue
le résultat est que la ligne suivante est fausse et ne créera pas de matrice symétrique :
>>> a += a.TAlgèbre linéaire :
le sous-module numpy.linalg implémente l'algèbre linéaire basique, pour résoudre les systèmes linéaires, la décomposition en valeurs singulières… Pour autant, il n'est pas garanti qu'il soit compilé en utilisant les routines optimales, et nous recommandons plutôt l'utilisation de scipy.linalg.
Exercice : autres opérations
- Regardez l'aide sur l'opération np.allclose. Quand cette opération peut-elle servir ?
- Regardez l'aide sur np.triu et np.tril.
II-B. Opérations de réduction▲
II-B-1. Calculer des sommes▲
Somme de lignes et de colonnes :
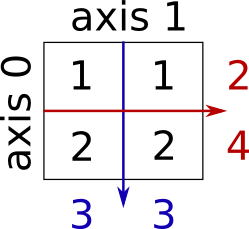
>>> x = np.array([[1, 1], [2, 2]])
>>> x
array([[1, 1],
[2, 2]])
>>> x.sum(axis=0) # columns (first dimension)
array([3, 3])
>>> x[:, 0].sum(), x[:, 1].sum()
(3, 3)
>>> x.sum(axis=1) # rows (second dimension)
array([2, 4])
>>> x[0, :].sum(), x[1, :].sum()
(2, 4)Dans le même genre, pour des tableaux de dimensions plus élevées :
II-B-2. Autres opérations de réduction▲
Extrema :
>>> x = np.array([1, 3, 2])
>>> x.min()
1
>>> x.max()
3
>>> x.argmin() # index of minimum
0
>>> x.argmax() # index of maximum
1Opérations logiques :
Comparaison de tableaux :
Statistiques :
>>> x = np.array([1, 2, 3, 1])
>>> y = np.array([[1, 2, 3], [5, 6, 1]])
>>> x.mean()
1.75
>>> np.median(x)
1.5
>>> np.median(y, axis=-1) # last axis
array([ 2., 5.])
>>> x.std() # full population standard dev.
0.82915619758884995Et beaucoup plus.
Exercice : réductions
- En dehors de sum, quelle autre fonction peut-on utiliser ?
- Quelle est la différence entre sum et cumsum ?
Exemple pratique : données statistiques
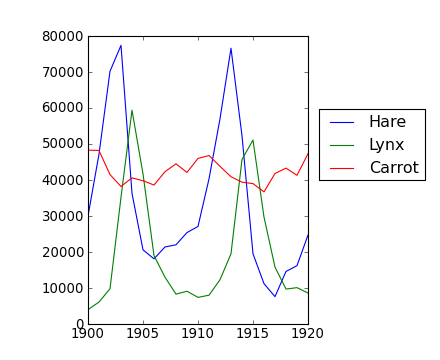
Les données contenues dans le fichier populations.txt décrivent les populations de lièvres et de lynx (et de carottes) dans le nord du Canada sur 20 ans.
Vous pouvez visualiser ces données dans un éditeur ou dans Ipython :
In [1]: !cat data/populations.txtPour commencer, chargez les données dans un tableau NumPy :
>>> data = np.loadtxt('data/populations.txt')
>>> year, hares, lynxes, carrots = data.T # trick: columns to variablesPuis affichez-les :
>>> from matplotlib import pyplot as plt
>>> plt.axes([0.2, 0.1, 0.5, 0.8])
>>> plt.plot(year, hares, year, lynxes, year, carrots)
>>> plt.legend(('Hare', 'Lynx', 'Carrot'), loc=(1.05, 0.5))La moyenne des populations dans le temps est :
>>> populations = data[:, 1:]
>>> populations.mean(axis=0)
array([ 34080.95238095, 20166.66666667, 42400. ])La variation moyenne est :
>>> populations.std(axis=0)
array([ 20897.90645809, 16254.59153691, 3322.50622558])Quelle espèce a la population la plus importante chaque année ?
>>> np.argmax(populations, axis=1)
array([2, 2, 0, 0, 1, 1, 2, 2, 2, 2, 2, 2, 0, 0, 0, 1, 2, 2, 2, 2, 2])Exemple pratique : broadcasting avec algorithme de marche aléatoire
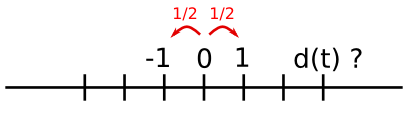
Considérons un simple algorithme de marche aléatoire unidimensionnel : à chaque pas de temps, nous avançons ou reculons, avec une probabilité similaire.
Nous allons ici tâcher de trouver la distance typique parcourue depuis le départ, après t sauts en avant ou en arrière.
Nous allons pour cela simuler plusieurs marcheurs pour trouver cette loi, et nous allons procéder à quelques simulations : nous allons créer un tableau 2D avec des histoires (chaque marcheur a sa propre histoire) avec sur une dimension le temps, et sur l'autre l'histoire.
>>> n_stories = 1000 # number of walkers
>>> t_max = 200 # time during which we follow the walkerNous allons choisir de manière totalement aléatoire si nous avançons ou reculons :
>>> t = np.arange(t_max)
>>> steps = 2 * np.random.random_integers(0, 1, (n_stories, t_max)) - 1
>>> np.unique(steps) # Verification: all steps are 1 or -1
array([-1, 1])Nous faisons avancer le marcheur en additionnant les pas dans le temps :
>>> positions = np.cumsum(steps, axis=1) # axis = 1: dimension of time
>>> sq_distance = positions**2Nous obtenons alors le fil conducteur de l'histoire :
>>> mean_sq_distance = np.mean(sq_distance, axis=0)On affiche le résultat :
>>> plt.figure(figsize=(4, 3))
<matplotlib.figure.Figure object at ...>
>>> plt.plot(t, np.sqrt(mean_sq_distance), 'g.', t, np.sqrt(t), 'y-')
[<matplotlib.lines.Line2D object at ...>, <matplotlib.lines.Line2D object at ...>]
>>> plt.xlabel(r"$t$")
<matplotlib.text.Text object at ...>
>>> plt.ylabel(r"$\sqrt{\langle (\delta x)^2 \rangle}$")
<matplotlib.text.Text object at ...>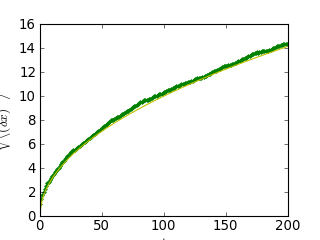
Nous venons d'établir un fait physique reconnu : la distance moyenne augmente proportionnellement avec la racine carrée du temps.
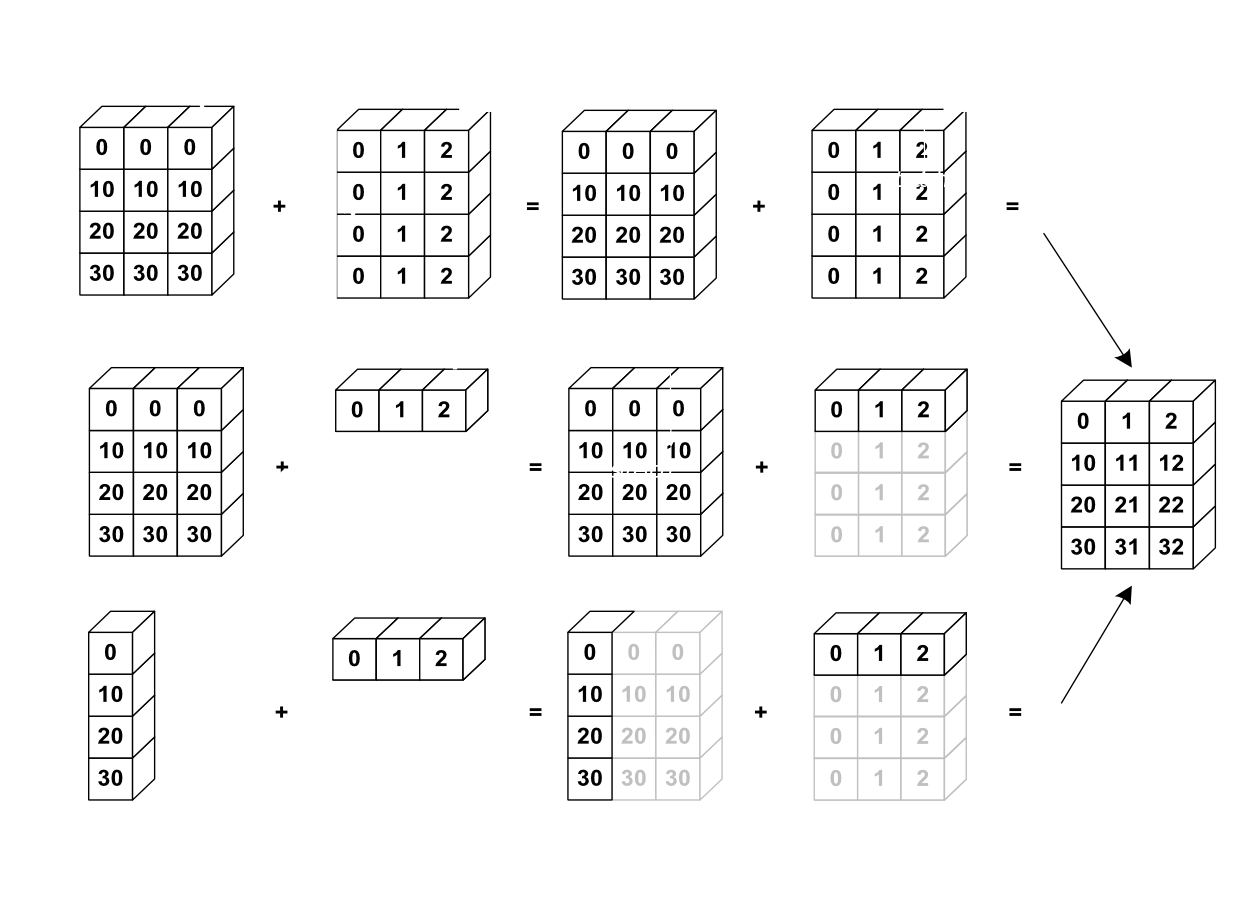
II-C. Broadcasting▲
- Les opérations basiques entre tableaux NumPy se font élément par élément.
- Cela ne fonctionne que sur des tableaux de dimensions identiques.
Dans tous les cas, il est possible d'effectuer les opérations entre des tableaux de tailles différentes si NumPy peut transformer ces tableaux de façon à ce qu'ils aient les mêmes dimensions. Cette conversion est alors appelée broadcasting.
L'image suivante donne un exemple de broadcasting :
Vérifions cela :
>>> a = np.tile(np.arange(0, 40, 10), (3, 1)).T
>>> a
array([[ 0, 0, 0],
[10, 10, 10],
[20, 20, 20],
[30, 30, 30]])
>>> b = np.array([0, 1, 2])
>>> a + b
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])Nous avons déjà fait du broadcasting sans le savoir :
>>> a = np.ones((4, 5))
>>> a[0] = 2 # we assign an array of dimension 0 to an array of dimension 1
>>> a
array([[ 2., 2., 2., 2., 2.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.],
[ 1., 1., 1., 1., 1.]])Une petite astuce fort utile :
>>> a = np.arange(0, 40, 10)
>>> a.shape
(4,)
>>> a = a[:, np.newaxis] # adds a new axis -> 2D array
>>> a.shape
(4, 1)
>>> a
array([[ 0],
[10],
[20],
[30]])
>>> a + b
array([[ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32]])Le broadcasting semble être un peu magique, mais il est en réalité tout naturel quand nous devons résoudre un problème dont les données de sortie sont un tableau avec plus de dimensions qu'en entrée.
Exemple pratique : broadcasting
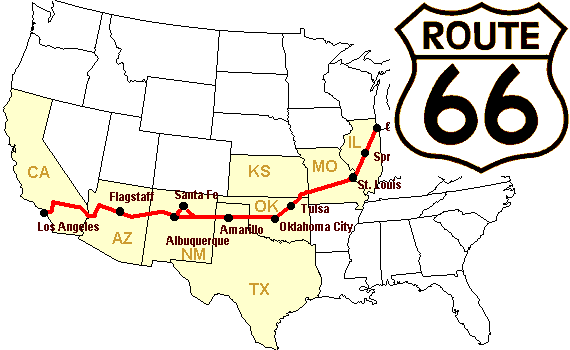
Nous allons construire un tableau des distances (en miles) entre chaque ville de la Route 66 : Chicago, Springfield, Saint-Louis, Tulsa, Oklahoma City, Amarillo, Santa Fe, Albuquerque, Flagstaff et Los Angeles.
>>> mileposts = np.array([0, 198, 303, 736, 871, 1175, 1475, 1544,
... 1913, 2448])
>>> distance_array = np.abs(mileposts - mileposts[:, np.newaxis])
>>> distance_array
array([[ 0, 198, 303, 736, 871, 1175, 1475, 1544, 1913, 2448],
[ 198, 0, 105, 538, 673, 977, 1277, 1346, 1715, 2250],
[ 303, 105, 0, 433, 568, 872, 1172, 1241, 1610, 2145],
[ 736, 538, 433, 0, 135, 439, 739, 808, 1177, 1712],
[ 871, 673, 568, 135, 0, 304, 604, 673, 1042, 1577],
[1175, 977, 872, 439, 304, 0, 300, 369, 738, 1273],
[1475, 1277, 1172, 739, 604, 300, 0, 69, 438, 973],
[1544, 1346, 1241, 808, 673, 369, 69, 0, 369, 904],
[1913, 1715, 1610, 1177, 1042, 738, 438, 369, 0, 535],
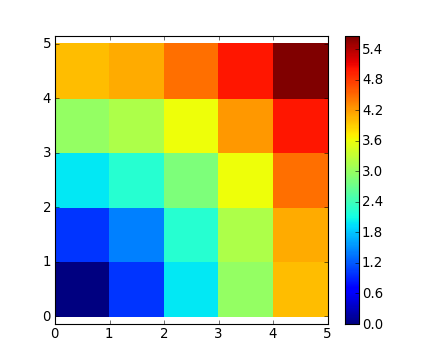
[2448, 2250, 2145, 1712, 1577, 1273, 973, 904, 535, 0]])Beaucoup de problèmes de calcul sur des grilles ou des réseaux peuvent être résolus par broadcasting. Par exemple, si nous désirons calculer la distance depuis l'origine jusqu'à chacun des points d'une grille de 10 x 10, nous ferons :
>>> x, y = np.arange(5), np.arange(5)[:, np.newaxis]
>>> distance = np.sqrt(x ** 2 + y ** 2)
>>> distance
array([[ 0. , 1. , 2. , 3. , 4. ],
[ 1. , 1.41421356, 2.23606798, 3.16227766, 4.12310563],
[ 2. , 2.23606798, 2.82842712, 3.60555128, 4.47213595],
[ 3. , 3.16227766, 3.60555128, 4.24264069, 5. ],
[ 4. , 4.12310563, 4.47213595, 5. , 5.65685425]])Ou en couleur :
>>> plt.pcolor(distance)
>>> plt.colorbar()Remarque : la fonction numpy.ogrid permet de créer directement les vecteurs x et y de l'exemple précédent, avec deux « dimensions significatives ».
>>> x, y = np.ogrid[0:5, 0:5]
>>> x, y
(array([[0],
[1],
[2],
[3],
[4]]), array([[0, 1, 2, 3, 4]]))
>>> x.shape, y.shape
((5, 1), (1, 5))
>>> distance = np.sqrt(x ** 2 + y ** 2)np.ogrid est très pratique dès que l'on désire effectuer des calculs sur une grille. D'un autre côté, np.mgrid fournit des matrices préremplies pour les cas où nous ne pouvons (où ne voulons) utiliser le broadcasting.
>>> x, y = np.mgrid[0:4, 0:4]
>>> x
array([[0, 0, 0, 0],
[1, 1, 1, 1],
[2, 2, 2, 2],
[3, 3, 3, 3]])
>>> y
array([[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3],
[0, 1, 2, 3]])II-D. Ajustement de tableaux▲
II-D-1. Aplatissement▲
>>> a = np.array([[1, 2, 3], [4, 5, 6]])
>>> a.ravel()
array([1, 2, 3, 4, 5, 6])
>>> a.T
array([[1, 4],
[2, 5],
[3, 6]])
>>> a.T.ravel()
array([1, 4, 2, 5, 3, 6])Pour les tableaux à plusieurs dimensions, c'est la dernière qui est défaite en premier.
II-D-2. Redimensionnement▲
L'inverse de l'opération précédente :
>>> a.shape
(2, 3)
>>> b = a.ravel()
>>> b = b.reshape((2, 3))
>>> b
array([[1, 2, 3],
[4, 5, 6]])Ou encore :
>>> a.reshape((2, -1)) # unspecified (-1) value is inferred
array([[1, 2, 3],
[4, 5, 6]])ndarray.reshape peut retourner une vue (cf. help(np.reshape)) ou une copie.
>>> b[0, 0] = 99
>>> a
array([[99, 2, 3],
[ 4, 5, 6]])Attention : reshape peut aussi retourner une copie :
>>> a = np.zeros((3, 2))
>>> b = a.T.reshape(3*2)
>>> b[0] = 9
>>> a
array([[ 0., 0.],
[ 0., 0.],
[ 0., 0.]])Pour bien comprendre cela, vous vous devez d'en apprendre plus sur la gestion de la couche mémoire des tableaux NumPy.
II-D-3. Ajout d'une dimension▲
L'indexation avec l'objet np.newaxis nous permet d'ajouter un axe à un tableau (relisez la section dédiée au broadcasting) :
>>> z = np.array([1, 2, 3])
>>> z
array([1, 2, 3])
>>> z[:, np.newaxis]
array([[1],
[2],
[3]])
>>> z[np.newaxis, :]
array([[1, 2, 3]])II-D-4. Réarrangement▲
>>> a = np.arange(4*3*2).reshape(4, 3, 2)
>>> a.shape
(4, 3, 2)
>>> a[0, 2, 1]
5
>>> b = a.transpose(1, 2, 0)
>>> b.shape
(3, 2, 4)
>>> b[2, 1, 0]
5Créer une vue :
>>> b[2, 1, 0] = -1
>>> a[0, 2, 1]
-1II-D-5. Redimensionnement avec resize▲
La taille d'un tableau peut être modifiée avec ndarray.resize :
>>> a = np.arange(4)
>>> a.resize((8,))
>>> a
array([0, 1, 2, 3, 0, 0, 0, 0])Il ne faut pas que le tableau soit référencé par autre chose :
>>> b = a
>>> a.resize((4,))
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: cannot resize an array that has been referenced or is
referencing another array in this way. Use the resize functionExercices : manipulation de structure
- Lisez la docstring concernant reshape, spécialement les notes de section à propos des copies et des vues.
- Utilisez flatten comme un substitut à ravel. Quelle est la différence ? (regardez laquelle renvoie une copie et l'autre une vue).
- Testez transpose.
II-E. Tri des données▲
Tri le long d'un axe :
>>> a = np.array([[4, 3, 5], [1, 2, 1]])
>>> b = np.sort(a, axis=1)
>>> b
array([[3, 4, 5],
[1, 1, 2]])Chaque ligne est triée séparément.
Tri in situ :
>>> a.sort(axis=1)
>>> a
array([[3, 4, 5],
[1, 1, 2]])Tri par indexation avancée (fancy indexing) :
>>> a = np.array([4, 3, 1, 2])
>>> j = np.argsort(a)
>>> j
array([2, 3, 1, 0])
>>> a[j]
array([1, 2, 3, 4])Trouver le minimum et le maximum :
>>> a = np.array([4, 3, 1, 2])
>>> j_max = np.argmax(a)
>>> j_min = np.argmin(a)
>>> j_max, j_min
(0, 2)Exercice : tri
- Testez le tri in situ et hors tableau.
- Essayez de créer des tableaux avec différents dtypes et triez-les.
- Utilisez all ou array_equal pour vérifier les résultats.
- Regardez np.random.shuffle comme moyen de créer des entrées triables.
- Combinez ravel, sort et reshape.
- Regardez le mot-clé axis pour sort et refaites l'exercice précédent.
II-F. En résumé▲
II-F-1. Qu'avez-vous besoin de savoir pour débuter ?▲
- Savoir comment créer des tableaux : array, arange, ones, zeros.
- Connaître la forme d'un tableau via array.shape, et savoir l'échantillonner pour obtenir différentes vues du tableau : array[::
2] … Ajuster la forme du tableau en utilisant reshape ou le remettre à plat avec ravel. - Obtenir un sous-ensemble du tableau et/ou modifier ses valeurs avec des masques :
>>> a[a < 0] = 0- Connaître les diverses opérations sur les tableaux, comme trouver la moyenne ou le maximum (array.max
(), array.mean()). Il n'est pas nécessaire de tout retenir, mais il faut avoir le réflexe de chercher dans la documentation (documentation en ligne,help(),lookfor()). - Pour un usage avancé : utiliser des outils comme le broadcasting. Connaître davantage de fonctions NumPy pour effectuer diverses opérations.
III. Allons un peu plus loin avec les tableaux NumPy▲
III-A. Types de données supplémentaires▲
III-A-1. Typage▲
Les types les plus importants ont la priorité dans les opérations mixtes entre types :
>>> np.array([1, 2, 3]) + 1.5
array([ 2.5, 3.5, 4.5])Les assignations ne changent jamais le type des données :
>>> a = np.array([1, 2, 3])
>>> a.dtype
dtype('int64')
>>> a[0] = 1.9 # <-- float is truncated to integer
>>> a
array([1, 2, 3])Typage forcé :
>>> a = np.array([1.7, 1.2, 1.6])
>>> b = a.astype(int) # <-- truncates to integer
>>> b
array([1, 1, 1])Arrondis :
>>> a = np.array([1.2, 1.5, 1.6, 2.5, 3.5, 4.5])
>>> b = np.around(a)
>>> b # still floating-point
array([ 1., 2., 2., 2., 4., 4.])
>>> c = np.around(a).astype(int)
>>> c
array([1, 2, 2, 2, 4, 4])III-A-2. Les différentes tailles de données▲
Entiers (signés) :
|
int8 |
8 bits. |
|
int16 |
16 bits. |
|
int32 |
32 bits (identique à int sur plateforme 32 bits). |
|
int64 |
64 bits (identique à int sur plateforme 64 bits). |
>>> np.array([1], dtype=int).dtype
dtype('int64')
>>> np.iinfo(np.int32).max, 2**31 - 1
(2147483647, 2147483647)
>>> np.iinfo(np.int64).max, 2**63 - 1
(9223372036854775807, 9223372036854775807L)Entiers non signés :
|
uint8 |
8 bits. |
|
uint16 |
16 bits. |
|
uint32 |
32 bits. |
|
uint64 |
64 bits. |
>>> np.iinfo(np.uint32).max, 2**32 - 1
(4294967295, 4294967295)
>>> np.iinfo(np.uint64).max, 2**64 - 1
(18446744073709551615L, 18446744073709551615L)Nombres à virgule flottante :
|
float16 |
16 bits. |
|
float32 |
32 bits. |
|
float64 |
64 bits (idem que les float). |
|
float96 |
96 bits, dépendant de la plateforme (np.longdouble). |
|
float128 |
128 bits, dépendant de la plateforme (np.longdouble). |
>>> np.finfo(np.float32).eps
1.1920929e-07
>>> np.finfo(np.float64).eps
2.2204460492503131e-16
>>> np.float32(1e-8) + np.float32(1) == 1
True
>>> np.float64(1e-8) + np.float64(1) == 1
FalseNombres complexes à virgule flottante :
|
complex64 |
2 float 32 bits. |
|
complex128 |
2 float 64 bits. |
|
complex192 |
2 float 96 bits. |
|
complex256 |
2 float 128 bits. |
Utilisation de types de données plus petits
Si vous ne savez pas que vous aurez besoin de types de données particuliers, c'est que vous n'en aurez probablement pas besoin.
Comparaison d'utilisation d'un float32 à la place d'un float64 :
- moitié moins de mémoire et d'espace disque utilisé ;
-
moitié moins de bande passante utilisée (opérations plus rapides en général)
SélectionnezIn [1]: a=np.zeros((1e6,), dtype=np.float64) In [2]: b=np.zeros((1e6,), dtype=np.float32) In [3]:%timeit a*a1000loops, best of3:1.78ms per loop In [4]:%timeit b*b1000loops, best of3:1.07ms per loop - mais : erreurs d'arrondi plus élevées, avec parfois des résultats imprévus.
III-B. Données structurées▲
|
sensor_code |
Chaînes de 4 caractères. |
|
position |
float. |
|
value |
float. |
>>> samples = np.zeros((6,), dtype=[('sensor_code', 'S4'),
... ('position', float), ('value', float)])
>>> samples.ndim
1
>>> samples.shape
(6,)
>>> samples.dtype.names
('sensor_code', 'position', 'value')
>>> samples[:] = [('ALFA', 1, 0.37), ('BETA', 1, 0.11), ('TAU', 1, 0.13),
... ('ALFA', 1.5, 0.37), ('ALFA', 3, 0.11), ('TAU', 1.2, 0.13)]
>>> samples
array([('ALFA', 1.0, 0.37), ('BETA', 1.0, 0.11), ('TAU', 1.0, 0.13),
('ALFA', 1.5, 0.37), ('ALFA', 3.0, 0.11), ('TAU', 1.2, 0.13)],
dtype=[('sensor_code', 'S4'), ('position', '<f8'), ('value', '<f8')])Les accès aux différents champs s'effectuent par indexation avec le nom du champ :
>>> samples['sensor_code']
array(['ALFA', 'BETA', 'TAU', 'ALFA', 'ALFA', 'TAU'],
dtype='|S4')
>>> samples['value']
array([ 0.37, 0.11, 0.13, 0.37, 0.11, 0.13])
>>> samples[0]
('ALFA', 1.0, 0.37)
>>> samples[0]['sensor_code'] = 'TAU'
>>> samples[0]
('TAU', 1.0, 0.37)Multiples accès à la fois :
>>> samples[['position', 'value']]
array([(1.0, 0.37), (1.0, 0.11), (1.0, 0.13), (1.5, 0.37), (3.0, 0.11),
(1.2, 0.13)],
dtype=[('position', '<f8'), ('value', '<f8')])L'indexation avancée fonctionne également :
>>> samples[samples['sensor_code'] == 'ALFA']
array([('ALFA', 1.5, 0.37), ('ALFA', 3.0, 0.11)],
dtype=[('sensor_code', 'S4'), ('position', '<f8'), ('value', '<f8')])Il existe beaucoup d'autres syntaxes. Voyez ICIhttp://docs.scipy.org/doc/numpy/user/basics.rec.html et ICIhttp://docs.scipy.org/doc/numpy/reference/arrays.dtypes.html#specifying-and-constructing-data-types.
III-C. maskedarray : tenir compte de données manquantes▲
Les masques fonctionnent pour tous les types :
>>> x = np.ma.array([1, 2, 3, 4], mask=[0, 1, 0, 1])
>>> x
masked_array(data = [1 -- 3 --],
mask = [False True False True],
fill_value = 999999)
>>> y = np.ma.array([1, 2, 3, 4], mask=[0, 1, 1, 1])
>>> x + y
masked_array(data = [2 -- -- --],
mask = [False True True True],
fill_value = 999999)Sur les fonctions usuelles :
>>> np.ma.sqrt([1, -1, 2, -2])
masked_array(data = [1.0 -- 1.41421356237 --],
mask = [False True False True],
fill_value = 1e+20)III-C-1. Bonnes pratiques▲
- Expliciter les noms des variables (cela signifie qu'il n'y aura pas besoin de commentaires pour dire à quoi correspond la variable).
- Respect du style : espace après les virgules, autour du symbole « = »… Un certain nombre de règles afin d'écrire du code « joli » (et afin que tout le monde utilise les mêmes conventions de codage) sont disponibles ICIhttp://www.python.org/dev/peps/pep-0008 et ICIhttp://www.python.org/dev/peps/pep-0257.
- À quelques exceptions près, les noms des variables et les commentaires doivent être en anglais.
IV. Opérations avancées▲
IV-A. Polynômes▲
NumPy est également capable d'effectuer des calculs sur des polynômes :
Par exemple kitxmlcodeinlinelatexdvp3x^2+2x-1finkitxmlcodeinlinelatexdvp :
>>> p = np.poly1d([3, 2, -1])
>>> p(0)
-1
>>> p.roots
array([-1. , 0.33333333])
>>> p.order
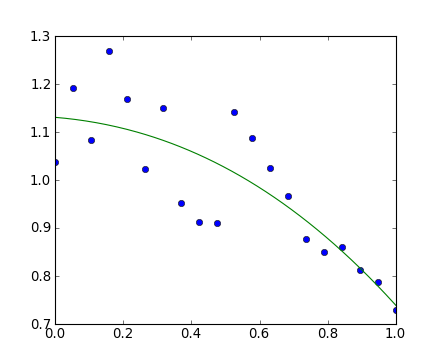
2>>> x = np.linspace(0, 1, 20)
>>> y = np.cos(x) + 0.3*np.random.rand(20)
>>> p = np.poly1d(np.polyfit(x, y, 3))
>>> t = np.linspace(0, 1, 200)
>>> plt.plot(x, y, 'o', t, p(t), '-')
[<matplotlib.lines.Line2D object at ...>, <matplotlib.lines.Line2D object at ...>]Voir http://docs.scipy.org/doc/numpy/reference/routines.polynomials.poly1d.html pour plus d'informations.
IV-A-1. Allons un peu plus loin▲
NumPy est également capable de calcul polynomial plus complexe, basé par exemple sur les polynômes de Chebychev. kitxmlcodeinlinelatexdvp3x^2+2x-1finkitxmlcodeinlinelatexdvp :
>>> p = np.polynomial.Polynomial([-1, 2, 3]) # coefs in different order!
>>> p(0)
-1.0
>>> p.roots()
array([-1. , 0.33333333])
>>> p.degree() # In general polynomials do not always expose 'order'
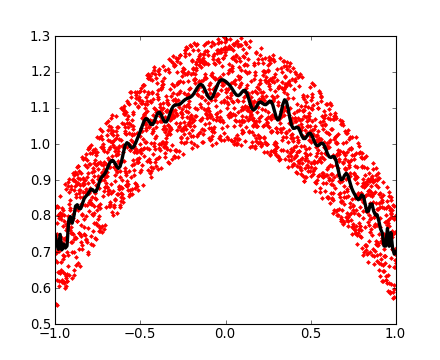
2Voici un exemple utilisant les polynômes de Chebyshev, sur l'intervalle [-1,1] :
>>> x = np.linspace(-1, 1, 2000)
>>> y = np.cos(x) + 0.3*np.random.rand(2000)
>>> p = np.polynomial.Chebyshev.fit(x, y, 90)
>>> t = np.linspace(-1, 1, 200)
>>> plt.plot(x, y, 'r.')
[<matplotlib.lines.Line2D object at ...>]
>>> plt.plot(t, p(t), 'k-', lw=3)
[<matplotlib.lines.Line2D object at ...>]Les polynômes de Chebychev sont très intéressants pour les calculs d'interpolations.
IV-B. Charger des fichiers de données▲
IV-B-1. Fichiers texte▲
Exemple : populations.txt
# year hare lynx carrot
1900 30e3 4e3 48300
1901 47.2e3 6.1e3 48200
1902 70.2e3 9.8e3 41500
1903 77.4e3 35.2e3 38200>>> data = np.loadtxt('data/populations.txt')
>>> data
array([[ 1900., 30000., 4000., 48300.],
[ 1901., 47200., 6100., 48200.],
[ 1902., 70200., 9800., 41500.],
...>>> np.savetxt('pop2.txt', data)
>>> data2 = np.loadtxt('pop2.txt')Si vous avez un fichier texte complexe, vous pouvez essayer :
- np.genfromtxt ;
- d'utiliser les fonctions d'E/S Python et, par exemple, les regexps pour parser le contenu (Python est plutôt bien équipé pour cela).
Rappelez-vous : naviguer dans le système de fichiers avec IPython
In [1]: pwd # show current directory
'/home/user/stuff/2011-numpy-tutorial'
In [2]: cd ex
'/home/user/stuff/2011-numpy-tutorial/ex'
In [3]: ls
populations.txt species.txtIV-B-2. Images▲
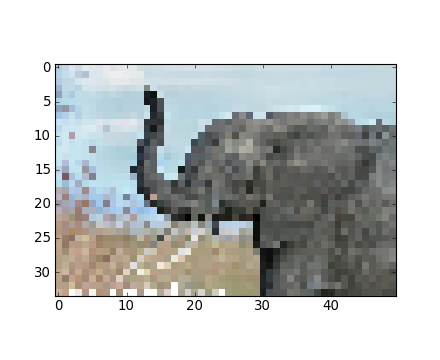
Avec Matplotlib :
>>> img = plt.imread('data/elephant.png')
>>> img.shape, img.dtype
((200, 300, 3), dtype('float32'))
>>> plt.imshow(img)
<matplotlib.image.AxesImage object at ...>
>>> plt.savefig('plot.png')
>>> plt.imsave('red_elephant', img[:,:,0], cmap=plt.cm.gray)En sauvegardant uniquement un canal (RGB) :
>>> plt.imshow(plt.imread('red_elephant.png'))
<matplotlib.image.AxesImage object at ...>Avec une autre bibliothèque :
>>> from scipy.misc import imsave
>>> imsave('tiny_elephant.png', img[::6,::6])
>>> plt.imshow(plt.imread('tiny_elephant.png'), interpolation='nearest')
<matplotlib.image.AxesImage object at ...>IV-B-3. Fichier au format NumPy▲
NumPy possède son propre format binaire, non portable, mais très efficace :
>>> data = np.ones((3, 3))
>>> np.save('pop.npy', data)
>>> data3 = np.load('pop.npy')IV-B-4. Autres formats courants▲
- HDF5 : h5pyhttp://code.google.com/p/h5py/, pyTableshttp://pytables.org/.
- NetCDF : scipy.io.netcdf_file, netcdf4-pythonhttp://code.google.com/p/netcdf4-python/…
- Matlab : scipy.io.loadmat, scipy.io.savemat.
- MatrixMarket : scipy.io.mmread.
… si quelqu'un l'utilise, il y a probablement une bibliothèque Python pour cela.
Exercice : fichiers texte de données
Écrivez un script Python qui charge les données depuis populations.txt et supprimez la dernière colonne et les cinq premières lignes. Enregistrez le jeu de données ainsi réduit dans pop2.txt.
Si vous êtes intéressé d'en apprendre plus sur les rouages internes de NumPy, je vous invite à lire les notions avancées de NumPyhttp://scipy-lectures.github.io/advanced/advanced_numpy/index.html#advanced-numpy.
V. Exercices▲
V-A. Manipulations de tableaux▲
1- Créez le tableau suivant (sans le saisir explicitement) et générez un nouveau tableau contenant sa 2e et 4e ligne.
[[1, 6, 11],
[2, 7, 12],
[3, 8, 13],
[4, 9, 14],
[5, 10, 15]]2- Divisez chaque colonne du tableau a, élément par élément, avec le tableau b. (astuce : np.newaxis).
>>> a = np.arange(25).reshape(5, 5)
>>> b = np.array([1., 5, 10, 15, 20])3- Un peu plus difficile : générez un tableau de 10 lignes de 3 colonnes avec des nombres aléatoires compris entre 0 et 1. Pour chaque ligne, extrayez le nombre le plus proche de 0,5.
- Utilisez abs et argsort pour trouver la colonne j la plus proche pour chaque ligne.
- Utilisez l'indexation avancée pour extraire les nombres. (astuce : a[i, j] ; le tableau i doit contenir le numéro de la colonne correspondante dans j).
V-B. Manipulation d'image : Lena▲
Effectuons quelques manipulations sur les tableaux NumPy en commençant par la célèbre image de Lena (http://www.cs.cmu.edu/~chuck/lennapg/). Scipy fournit un tableau 2D de cette image avec la fonction scipy.lena :
>>> from scipy import misc
>>> lena = misc.lena()Pour les versions anciennes de Scipy, utilisez scipy.lena().
Voici quelques images montrant ce que l'on peut obtenir avec quelques manipulations : utilisations de palettes de couleurs, rognage ou encore modification partielle de l'image.
-
Commençons par utiliser la fonction imshow pour afficher l'image
SélectionnezIn [3]:importpylabasplt In [4]: lena=misc.lena() In [5]: plt.imshow(lena) -
Lena est affichée en fausse couleur. Une palette de couleurs doit être précisée pour l'afficher en niveaux de gris.
SélectionnezIn [6]: plt.imshow(lena, cmap=plt.cm.gray) -
Créez un tableau à partir de l'image : par exemple, retirez 30 pixels en bordure de l'image. Pour visualiser le résultat, utilisez à nouveau imshow.
SélectionnezIn [9]: crop_lena=lena[30:-30,30:-30] -
Nous allons maintenant styliser le visage de Lena avec une marquise noire. Pour cela, nous avons besoin de créer un masque correspondant aux pixels que nous désirons colorer en noir. Ce masque est défini par la condition (y-256)**2 + (x-256)**2.
SélectionnezIn [15]: y, x=np.ogrid[0:512,0:512]# x and y indices of pixelsIn [16]: y.shape, x.shape Out[16]:((512,1),(1,512)) In [17]: centerx, centery=(256,256)# center of the imageIn [18]: mask=((y-centery)**2+(x-centerx)**2)>230**2# circle -
Ensuite, nous assignons la valeur 0 aux pixels de l'image correspondant à ce masque. La syntaxe est extrêmement simple et intuitive.
SélectionnezIn [19]: lena[mask]=0In [20]: plt.imshow(lena) Out[20]:<matplotlib.image.AxesImage object at0xa36534c>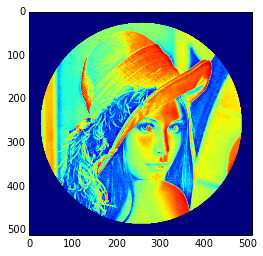
-
Copiez toutes les instructions de cet exercice dans un script que vous nommerez lena_locket.py, puis exécutez-le.
- Remplacez le cercle par une ellipse.
V-C. Statistiques de données▲
Les données contenues dans le fichier populations.txt décrivent les populations de lièvres et de lynx (et de carottes) dans le nord du Canada sur 20 ans.
>>> data = np.loadtxt('data/populations.txt')
>>> year, hares, lynxes, carrots = data.T # trick: columns to variables
>>> plt.axes([0.2, 0.1, 0.5, 0.8])
<matplotlib.axes.Axes object at ...>
>>> plt.plot(year, hares, year, lynxes, year, carrots)
[<matplotlib.lines.Line2D object at ...>, ...]
>>> plt.legend(('Hare', 'Lynx', 'Carrot'), loc=(1.05, 0.5))
<matplotlib.legend.Legend object at ...>Calculez et affichez à partir du jeu de données fourni :
- la moyenne de la population pour chaque espèce, pour chaque année de la période ;
- l'année pour laquelle chaque espèce a atteint son maximum de population ;
- quelle espèce a la population la plus importante pour chaque année (astuce : argsort et indexation avancée ) ;
- quelles années aucune des espèces citées ne dépasse les 50 000 (astuce : comparaisons et np.any) ;
- les deux années pour chaque espèce, où elles disposent de la population la plus basse (astuce : argsort, indexation avancée) ;
- comparez (graphique) l'évolution de la population de lièvres (voir
help(np.gradient)) et de lynx. Vérifier la corrélation (voirherlp(np.corrcoef)).
…Le tout sans faire la moindre boucle for.
V-D. Approximations d'intégrales brutes▲
Écrivez une fonction f(a,b,c) qui retourne ab-c. Créez un tableau de 24x12x6 contenant les valeurs de la fonction calculées dans le domaine [0,1]x[0,1]x[0,1].
Approchez la valeur de l'intégrale triple :
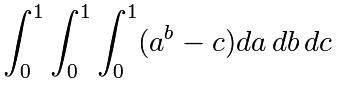
Le résultat exact est ![]() . Quelle est l'erreur relative ?
. Quelle est l'erreur relative ?
(Astuces : utilisez les opérations élément par élément et le broadcasting). Vous pouvez utiliser np.grid qui fournit un nombre de points dans un intervalle avec np.ogrid[0:1:20j]).
Rappelez-vous de la fonction Python :
def f(a, b, c):
return some_resultV-E. Jeu de Mandelbrot▲
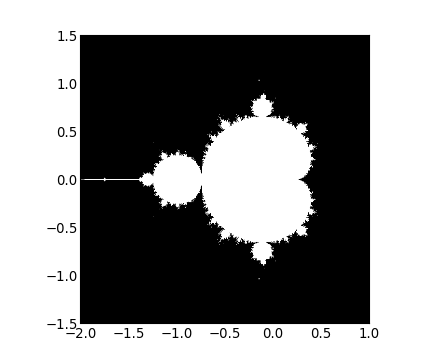
Écrivez un script qui calcule la fractale de Mandelbrot. L'itération de Mandelbrot est la suivante :
N_max = 50
some_threshold = 50
c = x + 1j*y
for j in xrange(N_max):
z = z**2 + cLes points (x, y) appartiennent à l'ensemble de Mandelbrot si |C| < some_threshold.
-
Effectuez ce calcul en suivant les étapes :
- construisez une grille de c=x+1j*y valeurs dans l'intervalle [-2,1]x[-1.5,1.5] ;
- effectuez l'itération ;
- créez le masque booléen 2D indiquant quels points appartiennent à l'ensemble ;
- sauvegardez le résultat dans une image avec :
>>> import matplotlib.pyplot as plt
>>> plt.imshow(mask.T, extent=[-2, 1, -1.5, 1.5])
<matplotlib.image.AxesImage object at ...>
>>> plt.gray()
>>> plt.savefig('mandelbrot.png')V-F. Chaîne de Markov▲
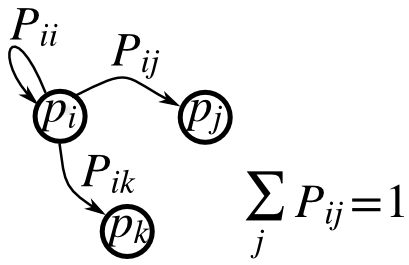
Soit P la matrice de transition d'une chaîne de Markov, et p la distribution des états :
- 0 <= P[i,j] <= 1 : la probabilité de passer de l'état i à l'état j ;
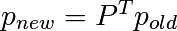 : la règle de transition ;
: la règle de transition ;- all
(sum(P, axis=1)==1), p.sum()==1: leur normalisation.
Écrivez un script pour une chaîne comportant cinq états qui :
- construit une matrice aléatoire et normalise chacune de ses lignes afin d'en faire une matrice de transition ;
- débute par une distribution (normalisée) aléatoire p et effectue 50 pas => p_50 ;
- calcule la distribution stationnaire : le vecteur propre de P.T associé à la valeur propre 1 (numériquement proche de 1) => p_stationary.
N'oubliez pas de normaliser le vecteur propre — Je ne l'ai pas fait…
- Vérifiez si p_50 et p_stationary sont égaux avec une tolérance de 1e-5.
Boite à outils : np.random.rand, .dot(), np.linlg.eig, réductions, abs(), argmin, comparaisons, all, np.linalg.norm, etc.
X. Remerciements▲
Merci aux personnes suivantes pour leur aide pour cette traduction :
Merci aux auteurs Emmanuelle GOUILLART, Didrik PINTE, Gaêl VAROQUAUX et Paul VIRTANEN pour avoir écrit ce tutoriel.